Guitar Fingerboard Combinatorics - An Analysis

In this article we will explore possible fingering configurations on the guitar fingerboard using combinatorics, a branch of mathematics that deals with counting and arrangement of objects.

Note - All technical terms are defined in the Glossary. When such a term first appears in the main body it will be bold and italicized so the reader will know to look for it in the Glossary if there exists any ambiguity about its meaning.

To begin with, we will choose three variables to define a field on the fingerboard to create our fingering configurations. We will choose how many frets along the fingerboard we will use, how many strings will be included, and how many different pitches will constitute each of the shapes created. A configuration is defined as a shape made with the left hand fingers on the fingerboard, and a configuration can consist of 2, 3 or 4 pitches per configuration (certainly we can have up to six pitches since there are six strings, but we will at first limit ourselves to four pitches in the first part of this article to work out the basic attributes of the configuration possibilities with four fingers, and later we will introduce barres).

A two-dimensional area of the fingerboard will be referred to as a field, with parameters defined by two variables: f = the number of frets that define the fingerboard field along the 'horizontal' axis of the fingerboard (along the length of the neck), and s = the number of adjacent strings that define the fingerboard field along the 'vertical' axis of the fingerboard (across the width of the neck). The s axis is orthogonal to the f axis, giving a two-dimensional field on the fingerboard. Within that fingerboard field, k = the number of pitches used for each configuration. It's important to realize that until we introduce barres, we can have more frets available than pitches, but not the other way around, so that k is always less than or equal to f, or k ≤ f. For example, we might have a fingerboard field that is four frets along the neck, or f = 4, but use only two fingers per configuration, or k = 2. It's clear we can make shapes with different numbers of pitches in any fingerboard field, and we will explore the possible configurations for many different values of f, s and k.

A further important point about k, or the number of pitches: Until we introduce barres, we will have only discrete configurations in which each of the fingers is on a different fret. This means that the use of two fingers on the same fret is disqualified with our first foray into non-barred configurations. Thus, in the first part of this article, "the number of pitches played" for each configuration is the same as saying "the number of fingers used" for each configuration. We'll look at this in greater detail below, but for now, I'll use k = fingers and k = pitches somewhat interchangeably for the moment.

With all this in mind, we reiterate that our variables will be:

For example, if we set the values f = 3, s = 2, then we would have a fingerboard field that looks like this:

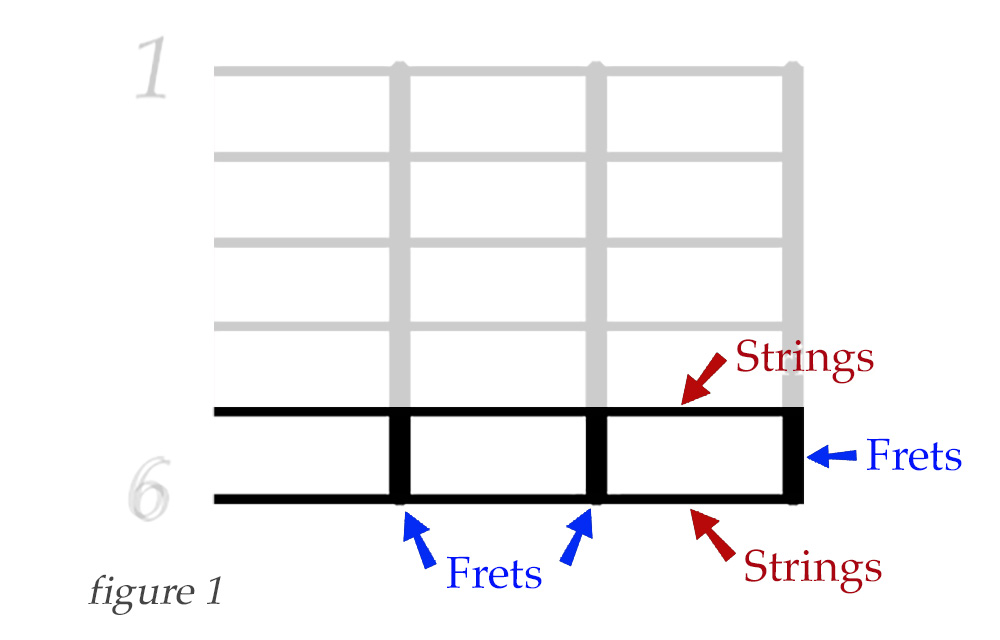
Note that this field is indicated by the strings and frets displayed in black, and can be placed anywhere on the neck. It can begin on any fret and will extend three frets along the neck, because f = 3. And since s = 2, we are using two strings, and the field can begin on string 6, 5, 4, 3, or 2. The 2nd string is the final possibility, because we need two adjacent strings, so beginning on the 2nd string would require strings 2 and 1.

Because the fingerboard field can be placed anywhere on the fingerboard where it will fit, we will just display the fields in our figures like this:

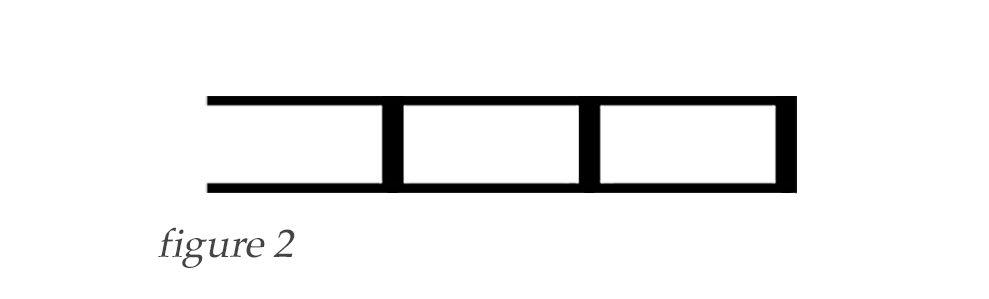
Now, let's set the k value to k = 2, which means we will initially use two fingers in each of our configurations. It also means each configuration will have two notes or pitches, played with two different fingers (until barres are introduced later). And, since we have already set f = 3 and s = 2 above, we have three frets and two strings to work with. It is clear that we will have multiple configurations arising from our two finger configurations in this fingerboard field.

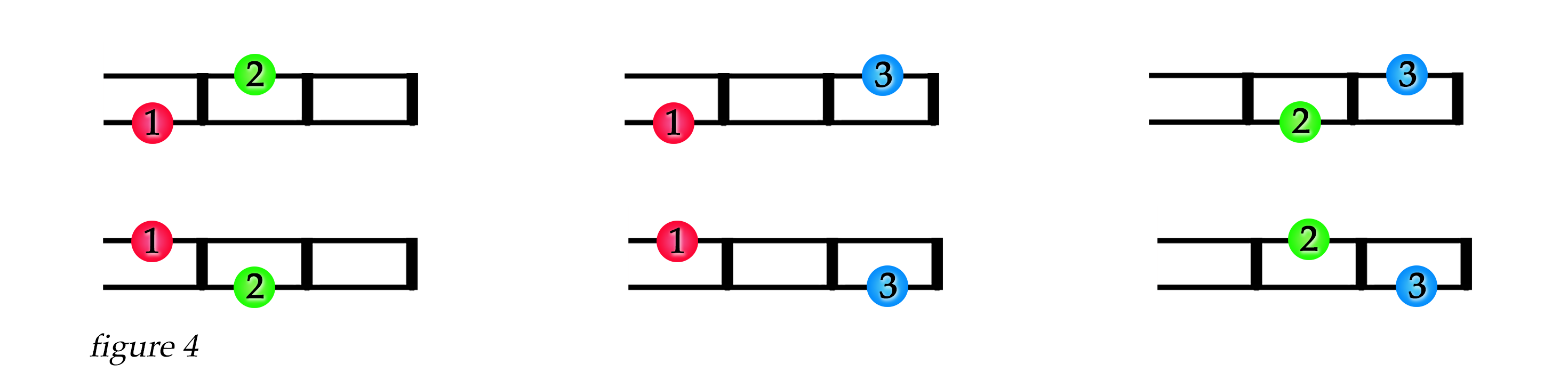
Without much thought, we realize two fingers at a time can be arranged three different ways, when we are drawing from a set of three fingers. With three fingers, our three combinations are $\{1,2\}$, $\{1,3\}$, and $\{2,3\}$. Figure 3 below shows us one way we can arrange these three combinations on the fingerboard. (Clearly we can invert the fingerings to double the amount of configurations in figure 3, but before we do that, let's look at the math that shows us how to find possible combinations of fingers.)

The formula used to find the possible combinations of a subset k from within a set of n elements, is called the binomial coefficient. The binomial coefficient is written

$$\left(\begin{array}{c}n\\ k\end{array}\right)$$

It is read as "n choose k", with n being the fixed set of elements and k being the subset of elements for which we want to find the possible combinations. For our calculation, n would represent the number of frets of the fingerboard field we are using, so for clarity we will change the n to an f to indicate the number of frets:

$$\left(\begin{array}{c}f\\ k\end{array}\right)$$

We will retain the variable k, since we have already designated k as the number of pitches we will use, and by using the binomial coefficient we will find how many configurations of k we can have for f.

However, the notation for the binomial coefficient is just a shorthand notation for the actual equation. Here is what the algebraic equation of the binomial coefficient actually is:

$$\left(\begin{array}{c}f\\ k\end{array}\right)=\frac{f!}{k!(f-k)!}$$

If you aren't familiar with factorials, the ! specifies a mutltiplication sequence. For example, n! means to multiply n * (n-1) * (n-2) . . . * 1. So 4! simply means to multiply 4 * 3 * 2 * 1, so 4! = 24.

Now let's plug in our values f = 3 and s=2 and see what we get.

$$\frac{3!}{2!(3-2)!}=\frac{3\ast 2\ast 1}{(2\ast 1)\ast 1}=\frac{6}{2}=3$$

So we see, we find three possible non-barred configurations of two fingers in a fingerboard field of three frets by using the binomial coefficient, which is what we illustrated above in figure 3.

However, we see immediately that we really have six combinations available here. Because we have two strings in our fingerboard field, we see we can invert each shape, giving us double the number of configurations. We will call the additional fingering arrangements made possible by the number of strings permutations. Since our example is a simple one, we can enivison the six configurations made possible by the permutations quite readily:

Clearly we need some additional calculation to show the correct number of configurations by including the value for s in our formula. After seeking an addition to the binomial coefficient that would give all possible non-barred configurations when also taking into account the number of strings used, I realized that I could put two binomial coefficients together for f and k, and s and k respectively.

$$\left(\begin{array}{c}f\\ k\end{array}\right)\left(\begin{array}{c}s\\ k\end{array}\right)k!$$

Though elegant in aspect, if we look closer at the actual equation this represents, we see that the added k! is redundant:

$$\left(\begin{array}{c}f\\ k\end{array}\right)\left(\begin{array}{c}s\\ k\end{array}\right)k!=(\frac{f!}{k!(f-k)!})(\frac{s!}{k!(s-k)!})k!$$

And can be reduced by cancelling the k! in either of the binomial coefficients:

$$(\frac{f!}{k!(f-k)!})(\frac{s!}{k!(s-k)!})k!=\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}=\left(\begin{array}{c}s\\ k\end{array}\right)\frac{f!}{(f-k)!}$$

So since they are equivalent, we can choose either $\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}$ or $\left(\begin{array}{c}s\\ k\end{array}\right)\frac{f!}{(f-k)!}$ to return the correct number of non-barred configurations, which we will designate with the letter A.

How did I arrive at this equation? As illustrated above, I knew that if we ignored the number of strings, the binomial coefficient was the most efficient way to express a combination of k fingers (pitches) used within a set of f frets. I also realized that the number of strings s had to be larger than or equal to the number of pitches played k, so s ≥ k. Here's why, and it's pretty intuitive: Each configuration contains k pitches, and I wanted each pitch to be able to be played simultaneously as a chord, so that we can hear each pitch in the configuration when plucked. Therefore, we must have enough strings s available to sound each pitch, since we can't simultaneously play two pitches on one string. And so, we need at minimum the same number of strings as pitches so that each pitch can be sounded simultaneously. So it is necessary that s ≥ k.

And since what we are really dealing with is a two-dimensional field on the fingerboard, the modification to the binomial coefficient must satisfy all conditions introduced by the extra dimension created by including multiple strings. I found that the series s * (s - 1) * ... * (s - (s - (k-1))), when multiplied by our binomial coefficient, satisfies our requirements for non-barred configurations. $$A=\left(\begin{array}{c}f\\ k\end{array}\right)(s\ast (s-1)\ast ...\ast (s-(s-(k-1))))$$

As an example, if s = 4 and k = 3, then the series above would be s * (s - 1) * (s - 2). The series stops at (s - 2) because that satisfies the last entry of the series (s - (s - (k-1))).

This series is actually what is called a 'falling factorial', and can also be much more compactly expressed with the product symbol as $$\prod _{i=0}^{k-1}(s-i)$$

But I realized I could also express this falling factorial without using either a series or the product operator Π. I could get the same result with the factor $\frac{s!}{(s-k)!}$ because $$\prod _{i=0}^{k-1}(s-i)=\frac{s!}{(s-k)!}$$

and I liked the similarity of $\frac{s!}{(s-k)!}$ to the binomial coefficient. I found this a more elegant notation, and this is how I derived the final equation to find non-barred configurations A: $$A=\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}$$

Remember that we stated above that $$\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}=\left(\begin{array}{c}s\\ k\end{array}\right)\frac{s!}{(f-k)!}$$

and so are equivalent to each other.

The two factors in both formulas $\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}$ or $\left(\begin{array}{c}s\\ k\end{array}\right)\frac{f!}{(f-k)!}$ represent combinations and permutations that when multiplied together, give us our total number of non-barred configurations. The binomial coefficient factors in each of the formulas $\left(\begin{array}{c}f\\ k\end{array}\right)$ and $\left(\begin{array}{c}s\\ k\end{array}\right)$ represent the combinations, which we will designate as $q_f$ and $q_s$ respectively, and the factors $\frac{s!}{(s-k)!}$ and $\frac{f!}{(f-k)!}$ represent the permutations, which we will designate as $p_s$ and $p_f$. This means we can also express our two equivalent formulas for non-barred configurations as a product of permutations and combinations on either factor, so non-barred configurations A can also be compactly expressed as $$A=(q_f)(p_s)=(q_s)(p_f)$$

If we extend the number of frets to four, so our variables are now f = 4, s = 2, and k = 2, we can plug in those values to our formula and it returns twelve possible configurations, as we see illustrated below in figure 5. This is also one of my warm-up exercises that I do across all strings, and it is what got me thinking about defining the possible configurations of the fingerboard mathematically.

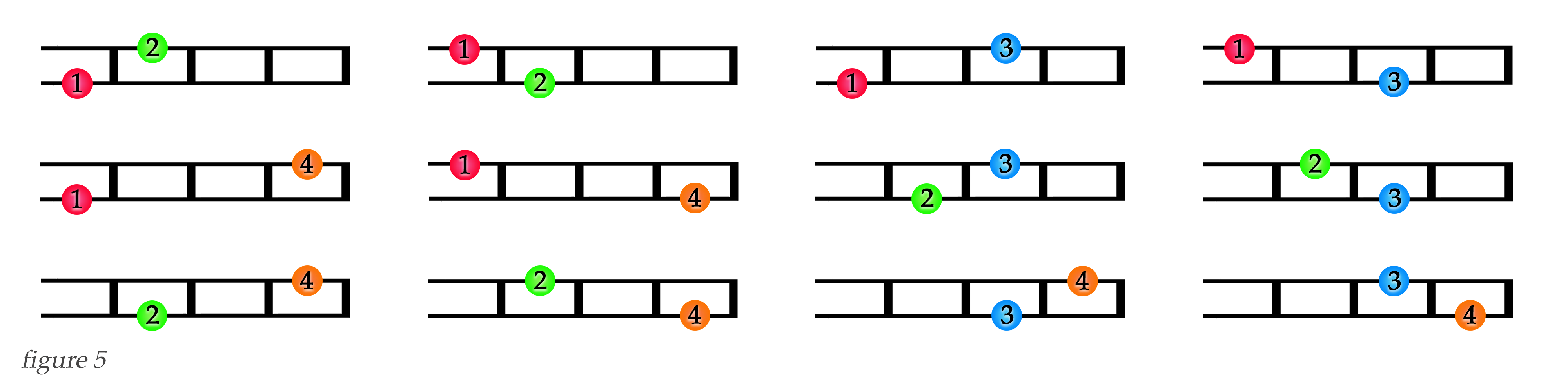
With four frets $f$ and using two fingers $k$ in each configuration, our binomial coefficient $\left(\begin{array}{c}f\\ k\end{array}\right)$ shows that we have six possible combinations within four frets $f$. Remember that combinations are designated by $q$, and we are using the number of frets $f$ to determing how many combinations $k$ we have, so here we have $q_f=\left(\begin{array}{c}f\\ k\end{array}\right)$. If we think of our combinations as subsets of a set, our set of four frets here is $\{1,2,3,4\}$, and from this set we can derive subsets of two fret combinations using two fingers at a time, or k = 2. With f = 4 and k = 2, $\left(\begin{array}{c}f\\ k\end{array}\right)=6$, with the subsets of the six combinations being $\{1,2\}$, $\{1,3\}$, $\{1,4\}$, $\{2,3\}$, $\{2,4\}$, and $\{3,4\}$. (With non-barred configurations, the numbers in these subsets mirror BOTH the fret combinations in the field and the finger numbers used to create them).

In figure 5 above we see that we have total configurations of $\left(\begin{array}{c}f\\ k\end{array}\right)\ast 2=12$, which is verified by including the number of permutations $p_s$ in our formula. Here the number of permutations $p_s=2$, and we know that $p_s=\frac{s!}{(s-k)!}$, so $$q_f\ast p_s=\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}=6\ast 2$$ which equals 12 configurations. This is because we have two strings, and each subset combination of $q_f$ can exist in two orientations on the two strings due to permutations $p_s$, giving us $q_f\ast p_s$ non-barred configurations.

Now let's take the same example as above in figure 5, but let's add one more string to see how our configurations develop.

Adding a third string to the example in figure 5 begins to exibit more complex behavior in the number of configurations available. This is because the number of configurations grow in a non-linear way as strings are added.

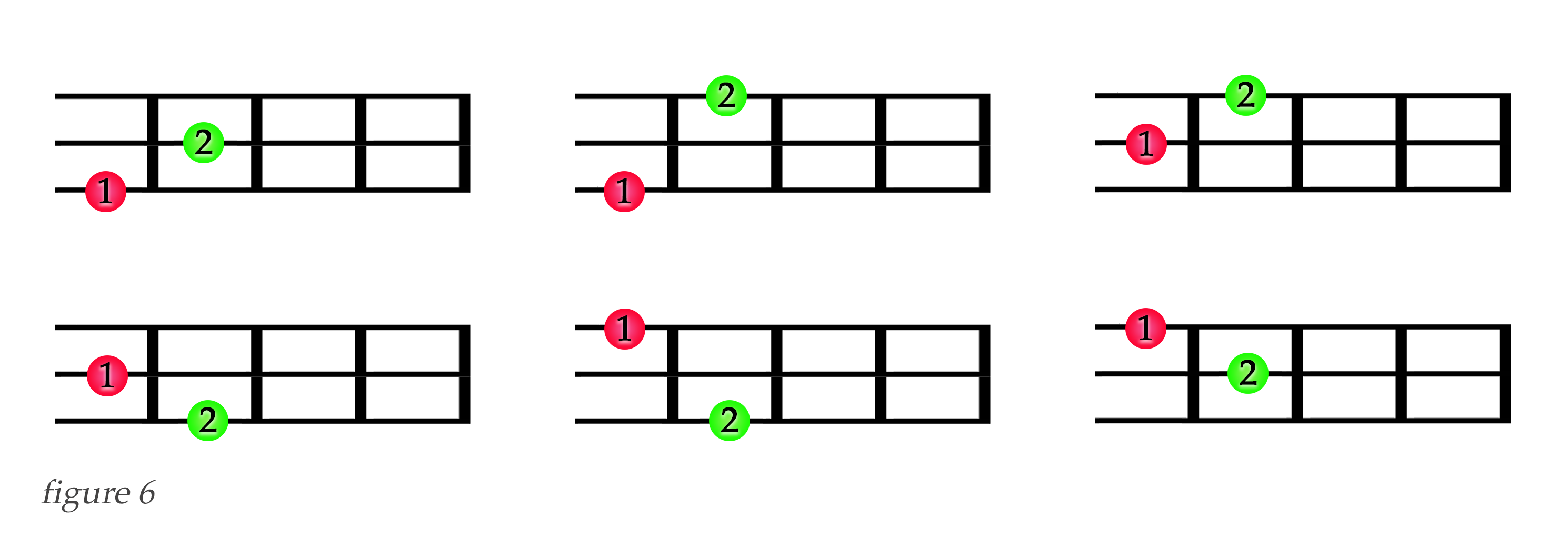
The rows in figure 6 show that because we have three strings available, there are now three possible ways to finger each single combination, here seen using just fingers 1 and 2. The columns show that each combination can be inverted, as we have also seen in figures 4 and 5. This means that we have six ways of playing each of the six subsets $\{1,2\}$, $\{1,3\}$, $\{1,4\}$, $\{2,3\}$, $\{2,4\}$, $\{3,4\}$ that are generated from the binomial coefficient for f = 4 and k = 2. With six subsets, and six ways of playing each subset, we have 6 * 6 = 36 configurations. And plugging in f = 4, s = 3 and k = 2 into our formula returns the value A = 36, showing our formula models this behavior perfectly.

Now let's ramp this all the way up to the maximum number of strings, s = 6. How many configurations are there for f = 4, s = 6 and k = 2? Entering the values for our variables into our formula, we have $$A=\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}=(\frac{4!}{2!(4-2)!})\frac{6!}{(6-2)!}=6\ast 30=180$$

giving us 180 configurations for two fingers across four frets and six strings.

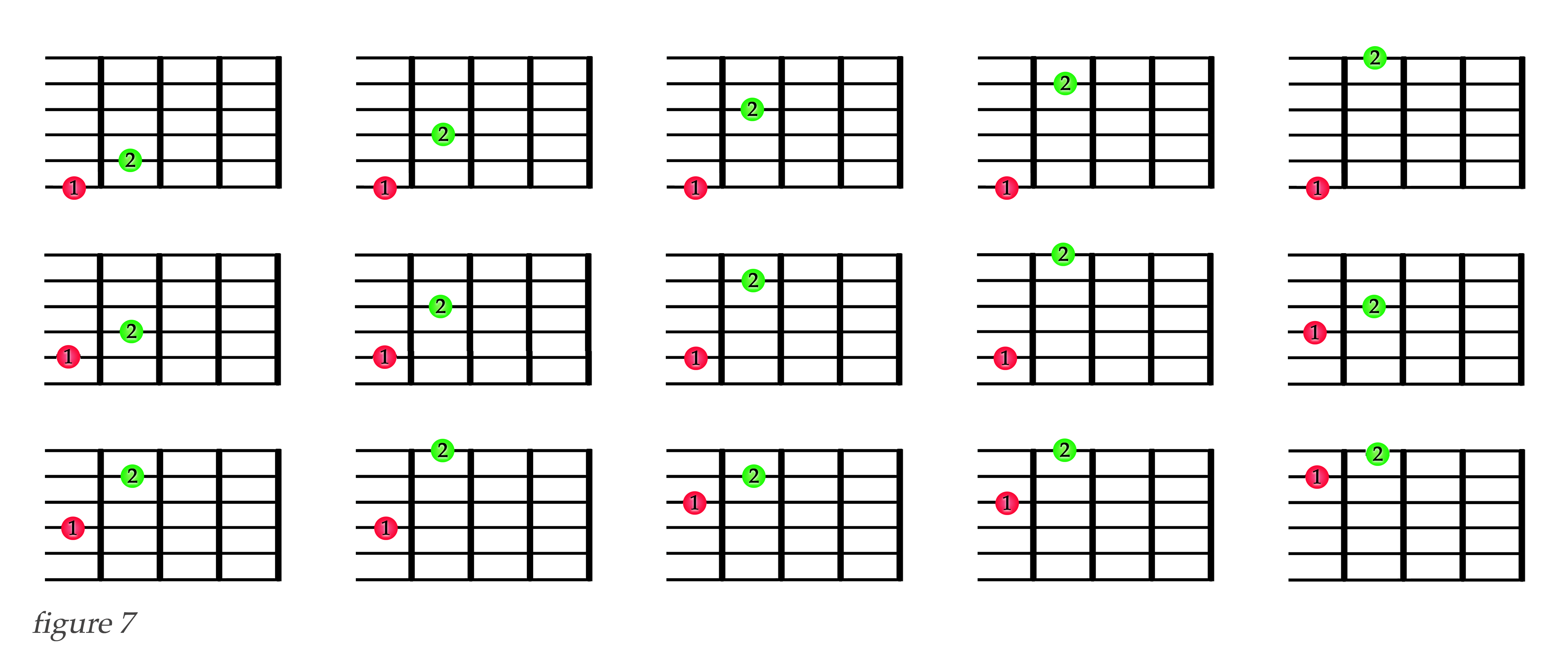
We can see this illustrated below in figure 7, just using finger configurations for only fingers 1 and 2. It shows how the number of strings affects the number of configurations by permutation, and by having six strings we have fifteen permutations of any single subset of 2 fingers. Keep in mind that in each of the fifteen combinations below, the position of fingers 1 and 2 can be inverted, giving a total of 30 permutated combinations. Figure 7 is a graphic illustration of the permutations $p_s$ from $\frac{s!}{(s-k)!}$, the part of our formula that takes the number of strings into account. When we multiply these 30 permutated combinations times the 6 subsets returned by $\left(\begin{array}{c}f\\ k\end{array}\right)$, we get the correct value of 180 configurations.

Now let's look at combinations with three fingers.

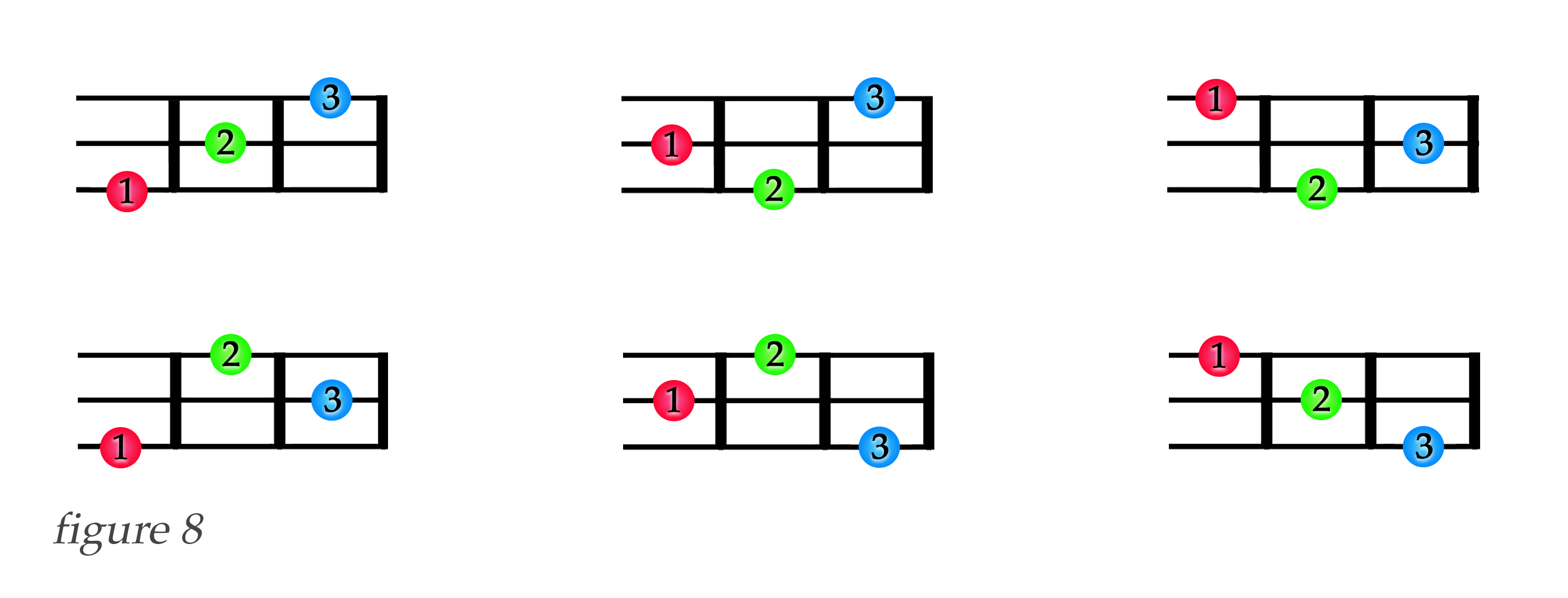
With three frets, three strings, and three fingers (pitches), $\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}$ tells us that we have six possible non-barred configurations, as illustrated in figure 8 below. [see technical note 1 below.]

If we add one more fret, giving us a fingerboard field with f = 4, it's not hard to see that we would have 24 configurations by looking at the combinations $q_f$ in figure 8b below (notice with four frets we can use the 4th finger too).

Since k = 3, and we are using three fingers at a time, the possible finger combinations $q_f$ with four frets is $\left(\begin{array}{c}4\\ 3\end{array}\right)=4$, which now gives us 24 configurations, because the six configurations shown in figure 8 are now multiplied by 4. This is because of the possible finger combinations here. If we again view these finger combinations as sets, then we see that besides the finger combination set $\{1,2,3\}$ shown above in figure 8, we also can have combination sets $\{1,2,4\}$, $\{1,3,4\}$ and $\{2,3,4\}$, as illustrated in figure 8b. Looking at the configuration permutations of set $\{1,2,3\}$ in figure 8, it's clear if we apply those same permutations to all four possible sets shown in figure 8b, we get 6 permutations times 4 sets, or 24 configurations. We can verify this by putting the values f = 4, s = 3 and k = 3 into our formula and we arrive at $$\left(\begin{array}{c}4\\ 3\end{array}\right)\frac{3!}{(3-3)!}=24.$$

If we take the upper left hand configuration in figure 8 above, and permutate only that configuration of 3 pitches along 4 frets (as we show in figure 8b), we see we have four possible ways to configure just that one configuration.

That represents each of the four sets we just created above. We can see that if we permutate each of these combinations in figure 8b six times, corresponding to the six different permutation possibilities in figure 8, we again show there are 24 configurations with f = 4, s = 3, and k = 3.

We can extend this to four, five and six strings as well. Let's go right to the maximum of six strings - with six strings and four frets, we would have f = 4, s = 6 and k = 3. Plugging these into our formula to find the number of total configurations A will return $$A=\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}=480$$ configurations. That's a lot. Plug in the variables and try the calculation yourself.

The concept is very straightforward now. With the larger number of configurations it's too unwieldy to illustrate in diagrams. But let's calculate configurations A using four fingers across the fingerboard, with a span of four frets, and six strings. That gives us four frets, six strings, and four fingers, so f = 4, s = 6 and k = 4. $$A=\left(\begin{array}{c}f\\ k\end{array}\right)\frac{s!}{(s-k)!}=\left(\begin{array}{c}4\\ 4\end{array}\right)\frac{6!}{(6-4)!}=360.$$ We can also add more than four frets. Try any combination with five frets, and it will return the configurations, but note that with more frets, there will be some configurations that may be difficult or impossible to finger.

You may have noticed that we have not yet included barres, or playing more than one note on a single fret, into our equations. Let's do that now, because barring is of course an integral part of chord fingering on the guitar.

A barred configuration will be defined as any configuration that includes two or more pitches on a single fret. The simplest example of this is with k = 2, and when using only two pitches per configuration, the only barre possibility is to play two pitches on the same fret. Depending on how many strings are used, the two pitches on the fret do not have to be on adjacent strings if s >2.

In figure 6 above, we saw that there are 36 unbarred configurations when f = 4, s = 3 and k = 2. Let's take a look at how many barred possibilities there are using the same parameters, as illustrated in figure 9 below.

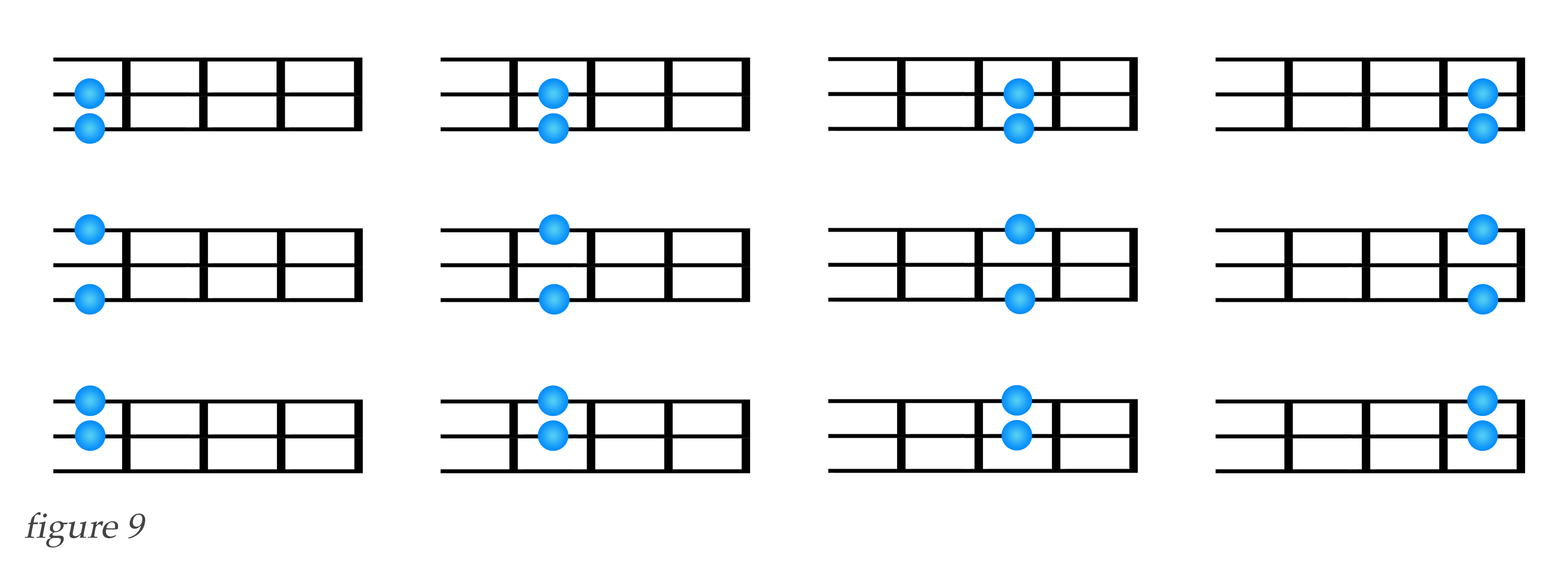
As we see, there are 12 barred configurations possible. So adding the barred and unbarred configurations , we have 12 + 36, or 48 total possible configurations for f = 4, s = 3 and k = 2.

Since our original formula only calculates the non-barred configurations, as we have seen in all our ealier examples, I've also developed a separate equation that returns the total number of configurations, both barred and unbarred. Here it is: $$C=\left(\begin{array}{c}s\\ k\end{array}\right)f^k$$

We can use this formula to calculate C, which will designate the TOTAL number configurations, both barred and unbarred, for any functional values of f, s and k.

An important distinction at this point: Since barres can be done with a single finger, or the pitches on the same fret can also sometimes be played with separate fingers, the actual fingers used become irrelevant in our configurations. Imagine two notes on the third fret, C on the 5th string, and G on the 1st string. We can barre both notes with the 1st finger, or can play the C with finger 1 and the G with finger 2, or with fingers 2 and 3, and so on, as we see in figure 10 below.

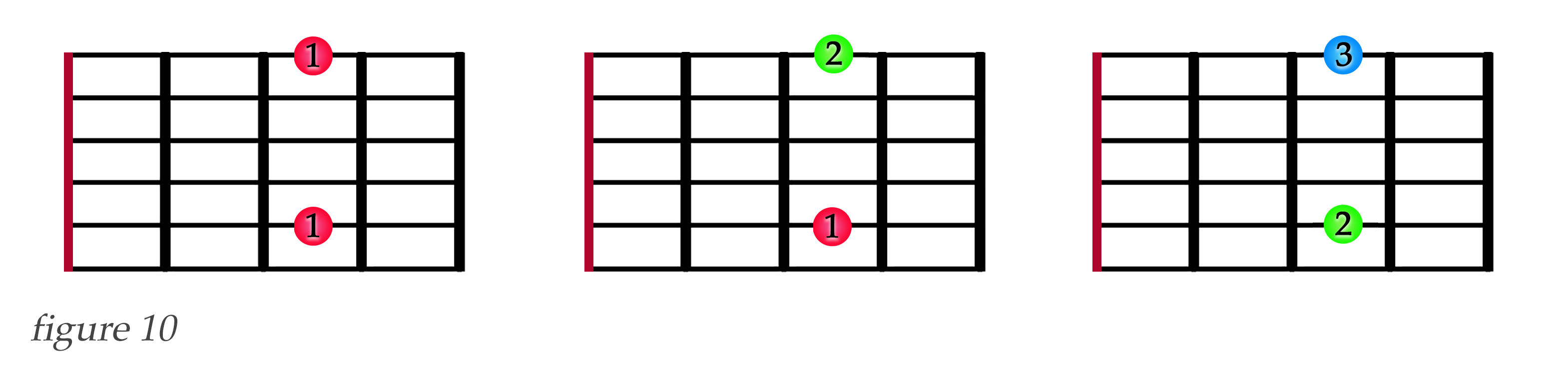
So from now on, we will now simply illustrate the frets being fingered by a colored dot without a finger number within the dot. But each pitch sounded within a barre counts toward our value of k. That means we also need to re-define k. k will no longer stand for the number of fingers, but instead for the number of pitches sounded to create a configuration. Figure 11 below shows some example configurations with k = 3 that includes our C - G barre. No matter how we finger them, each configuration must have only three sounding pitches, because k = 3.

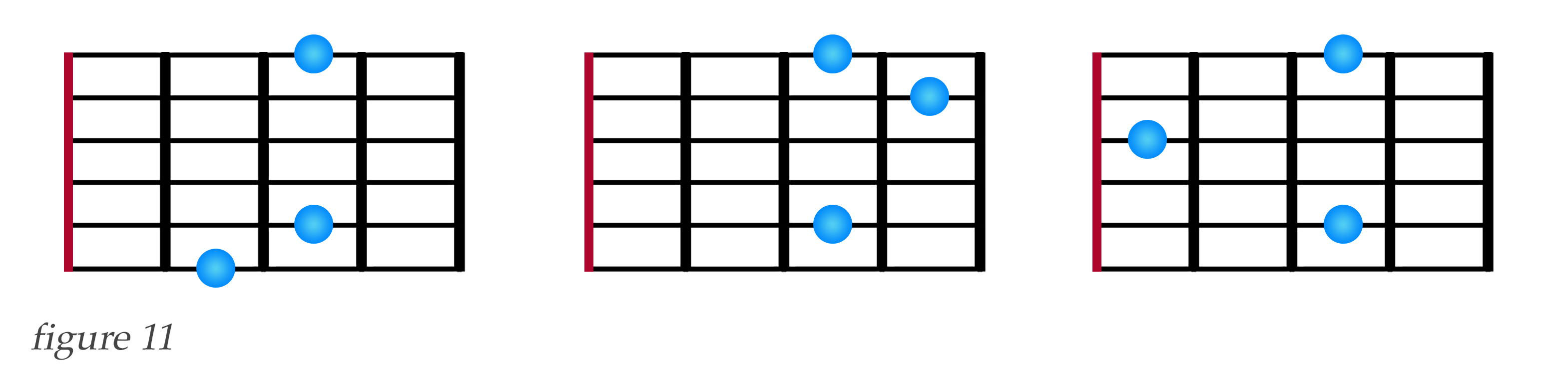
Of course, we can also have three notes in the barre, or four when k = 4. However, if we want to include configurations that have more pitches than there are frets, or $k>f,$ then there is a caveat: Our A equation will now be undefined, and we can't use it. But that is alright, and here is an example why.

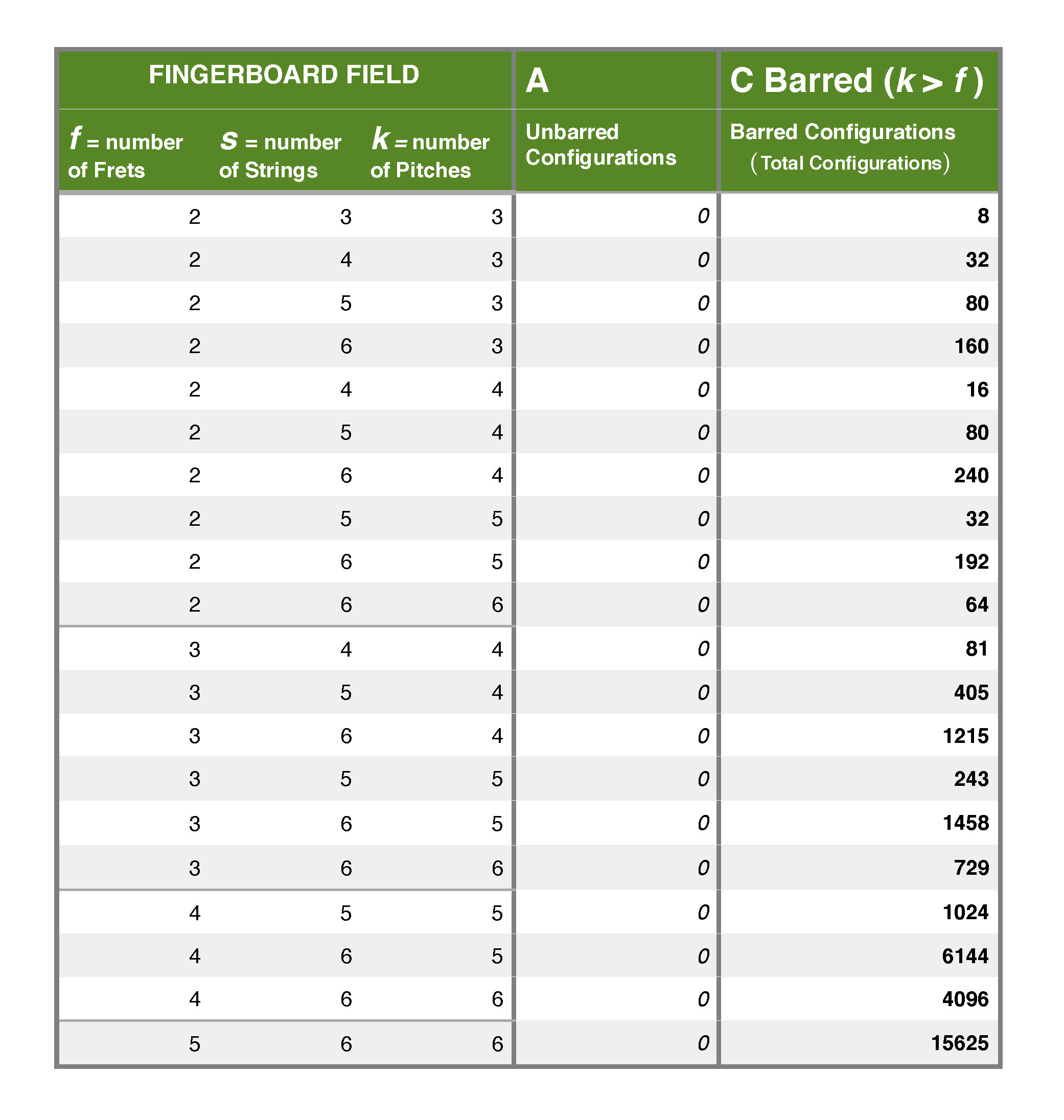
If we have, for example, f = 2, s = 6, and k = 6, then that is telling us we want to play six pitches in our configurations. But if we only have two frets in our fingerboard field, then the only configurations that can exist would be a barre. This is because six pitches crammed into two frets (and six strings) would by necessity have multiple pitches on a fret, which we have defined as a barre. In fact, with six pitches in a two fret space, we would have to use all six strings every time, and every single configuration would have to be a barre, either on one fret or both! So there are no possible non-barred configurations available in cases where $k>f,$ and we cannot use the A formula, as it would be undefined. The C formula returns the correct number of barres when $k>f.$ In this example, when f = 2, s = 6, and k = 6, our C formula returns a value of 64, which is the correct number of barred configurations.

However, how can we find just the barred configurations for all functional values of f, s, and k?

I've used some algebraic sleight of hand to remove the undefined situations, allowing us to return only the barred configuration as needed. I created a binary "switch" that solves this problem. We'll call the switch $\lambda$.

$$\lambda =\frac{((k-f)-|k-f|)-1}{1-2(k-f)}$$

And the full equation to return only the barred configurations is

$$B=\left(\begin{array}{c}s\\ k\end{array}\right)(f^k-\left(\frac{f!}{|f-k|!}\right)\left(\frac{-\lambda +1}{2}\right))$$

In the equation above for finding B, the factor on the right side is functioning as a binary switch that turns off the factor $\frac{f!}{|f-k|!}$ in all situations when it is not necessary in the equation, and any value other than zero returned by this factor would result in an incorrect number for the barred configurations. As we have seen, this factor is unnecessary when $k>f,$ because that is when the C formula $\left(\begin{array}{c}s\\ k\end{array}\right)f^k$ returns only the barred configurations (which is also the total configurations when $k>f$). Looking closely at the B formula above, we see that the first two elements are precisely the same as the C formula in its entirety, and so we do not need the factor $\frac{f!}{|f-k|!}$ at all, and it must be turned off by the binary switch I have devised. I like making equations that behave a little like algorithms by having parts of the equation change the method of functionality of the entire equation at certain internal values, and that is what I have done by employing a binary switch.

An important point to reiterate: When $k>f,$ then only configurations containing barres are possible, simply because there are more pitches k in a configuration than there are frets f in the fingerboard field, so by necessity two or more pitches must occur on at least one fret. So when $k>f$ and we employ our C equation, all the configurations are barred. This makes the total number of configurations when $k>f$ identical to the number of barred configurations, so C = B when $k>f.$ But we can always use our B equation above for retrieving barred configurations in all situations.

Armed with our new formulas, we can extract the number of barred, unbarred, and total configurations by utilizing three different equations:

And there we have the final formulas to include all configurations for different values of f, s and k, completing our analysis of fingerboard combinatorics.

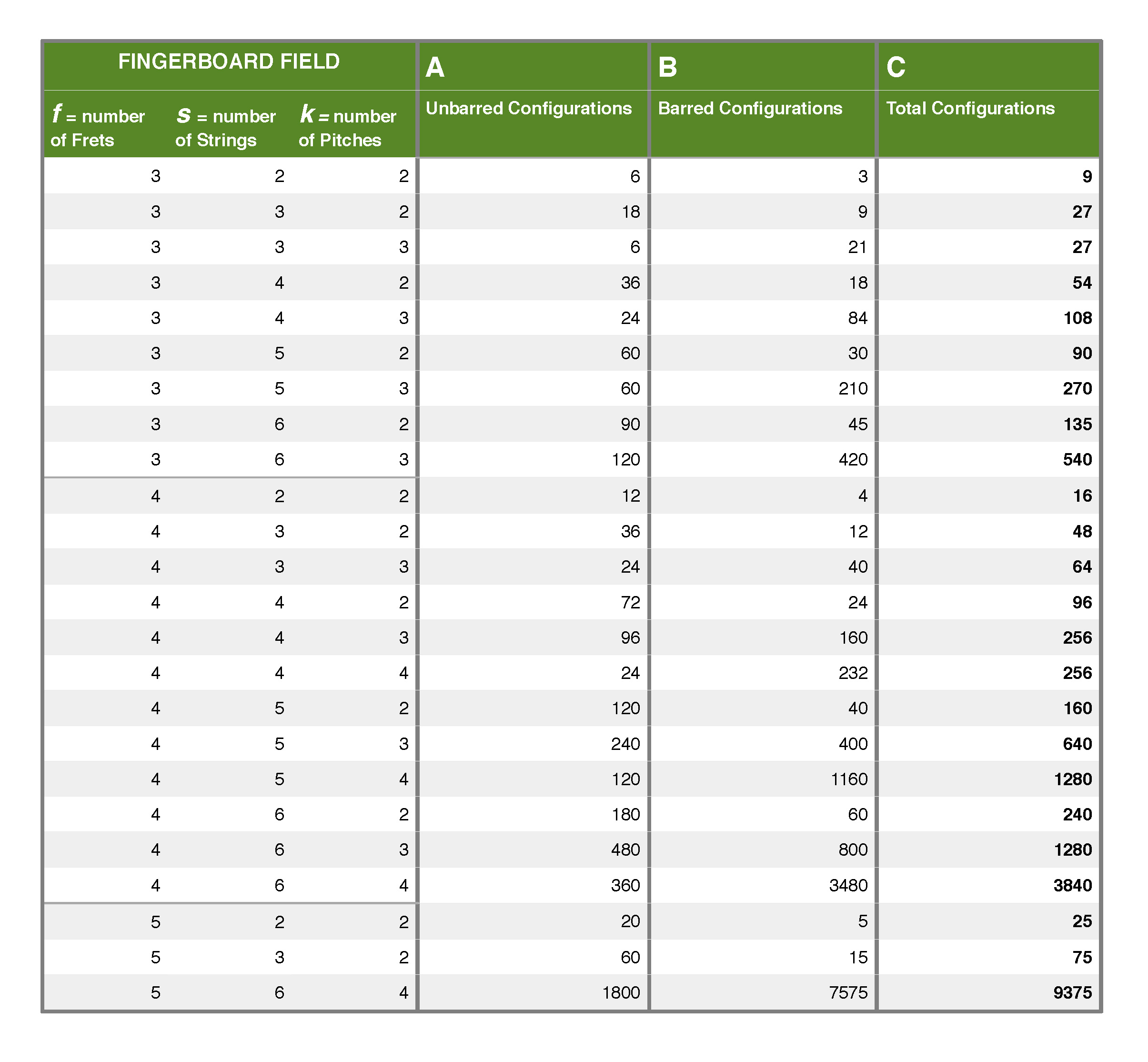
To conclude, we have a chart below illustrating the possible barred and unbarred configurations for a selection of values of frets, strings and pitches, as well as the total configurations for each set of values.

Acknowledgments

Thanks to John Olson for his perceptive advice and for bringing great clarity to some of the concepts, and to Oscar Azaret and Rich Coco for their excellent suggestions.

Glossary

Technical Note 1: In example 8, $\left(\begin{array}{c}f\\ k\end{array}\right)$ is $\left(\begin{array}{c}3\\ 3\end{array}\right)$. This gives us $$\left(\begin{array}{c}3\\ 3\end{array}\right)=(\frac{3!}{3!(3-3)!})=\frac{6}{6\ast 0!}$$ You'll notice we have 0! on the bottom of the binomial coefficient formula, and you may not know what to make of that. The mathematical convention for 0! is 0!=1, for certain reasons. So the value here of $\left(\begin{array}{c}3\\ 3\end{array}\right)=1$.