
There's something strange about the way mirrors reflect, if they are moving really fast. The angle of reflection is not what we were taught, when observed from another frame of reference. So say the equations. In fact, it happens anytime a mirror is in motion, but only becomes apparent at relativistic velocities.
Let's follow up on this phenomenon. I became interested in bouncing light around in spaceships, specifically spaceships that can go at relativistic speeds, or a significant portion of the speed of light. (See my article on Terrell Rotation for another exploration into relativistic effects). Bouncing light is often done in examples to illustrate a 'light clock' that demomstrates time dilation and length contraction at relativistic velocities. However, I noticed that almost always, the light was bounced in one of two directions - parallel to the direction of motion, or ninety degrees from that, perpendicular to the direction of motion. Admittedly this makes the computations slightly simpler. However, for a thought experiment, I thought it would be interesting to bounce the light off a mirror in a spaceship that returns the light pulse back to the ship's occupant, and be able to send the light pulse at any angle, and have the mirror angled appropriately to send the bounced light back.
And therein lay the problem - the solution to these equations suggested something unexpected about the angle of reflection from a mirror in motion.
So let's dive in. To explore this, we have a circular spacehip, and the occupant is sitting at the center \(m,\) which at rest is \(x = 0\) and \(y = 0.\) The light pulse generator is the red tube located in the ship's center along with the occupant, and the mirror is at the edge of the spaceship, bouncing the light straight back to the occupant observer. The distance the light travels \(\tau\) is also a description of proper time, the time we see elapse as outside observers, as the light proceeds to the mirror, and then back to the occupant.
We will consider mirror placement anywhere from 90º (straight up from occupant along y-axis) to 0º (straight forward from occupant along the x-axis). In figure 1 below, we show three possible placements of the mirror angle \(\alpha\) and light pulse angle \(\theta,\) where \(\alpha\) = 0º, -30º and -90 º, and \(\theta\) = 90º, 60º and 0º. Note that \(\alpha\) always equals \(\theta - 90º.\)
figure 1, ship at rest showing mirror and occupant
We'll give our circular ship a radius with a unit of 1, which will allow us to easily use trigonometric calculations for the changing angles of the mirror and light pulse trajectory. Moreover, we'll consider the radius of the ship to be one light-second to allow the phenomena to be simply expressed, even though that is an absurdly large size for a spaceship. But no matter, the calculated results can be scaled for any size ship, but it is best for clarity to keep the radius at \(r = 1\) light-second.
One thing we have to remember is that within a frame of reference, everything must always seem the same to the observer within that reference frame, regardless of velocity as perceived by another observer outside that reference frame. So, the spaceship's occupant will experience that the light pulse always travels directly to the mirror at angle \(\theta,\) and always bounces directly back, and always takes the same amount of time doing so, and it doesn't matter at what velocity the ship is traveling. But we, with our outside perspective, will measure something quite different happening with the trajectory and timing of the light pulse, depending on the velocity of the ship as it goes by.
For the simplest example, as is often shown in explanations about the effects of relativistic speeds on light propagation, we'll put our mirror straight 'up' from the occupant, perpendicular to the direction of motion. Our occupant will be sitting in the center of the ship, and the mirror will be at angle \(\alpha = 0º,\) because it is simply bouncing the light straight back down to the occupant. First we'll look at the simple situation of the ship at rest, and witness the light simply going straight up and bouncing straight back down to the ship's occupant, with an angle of the light pulse \(\theta\) at 90º.
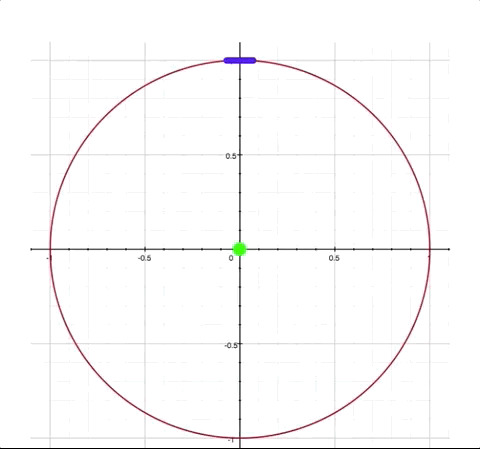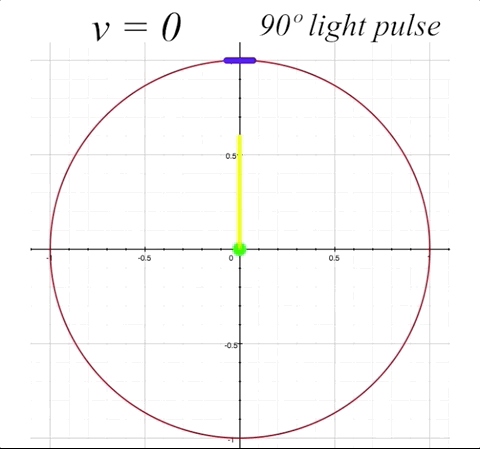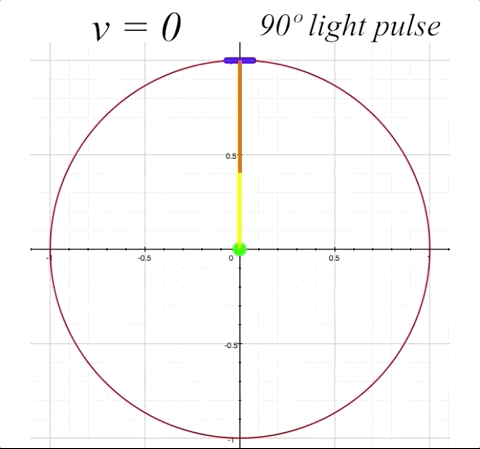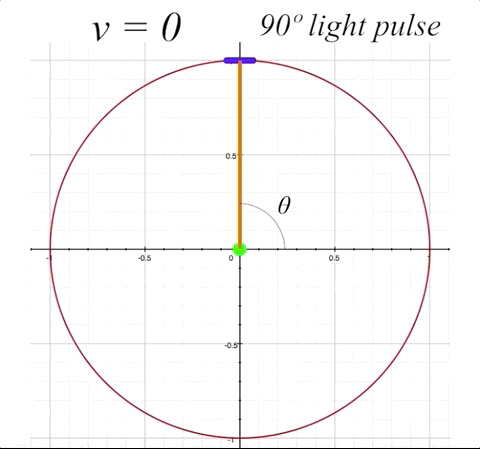
Now we will send our ship along at \(v = 0.5\), or half the speed of light (with \(v = 0\) being velocity zero (at rest), and \(v = 1\) representing lightspeed, where \(1 = c.\) The mirror is still situated straight up at 90º from the occupant. By having the mirror angle \(\alpha\) horizontal to the x-axis (which is the direction of motion), there will be no change in the mirror's angle due to length contraction. But we will get a good sense of how the angle of light pulse propation within the ship changes from the perspective of an outside observer when the ship is in motion. The light pulse angle will no longer be the rest angle \(\theta.\) Instead, when the ship is in motion, the resultant light pulse angles (both toward the mirror and the return reflection) change from an external observer's perspective. We will label these changed angles \(\zeta_1\) for the angle of outgoing light pulse, and \(\zeta_2\) for angle of the reflected light pulse that returns to occupant. Both \(\zeta_1\) and \(\zeta_2\) will now be visible to us as outside observers. Notice that \(\zeta_1\) is determined by its angle in relation to the x-axis, and \(\zeta_2\) is determined by its angle in relation to the y-axis.
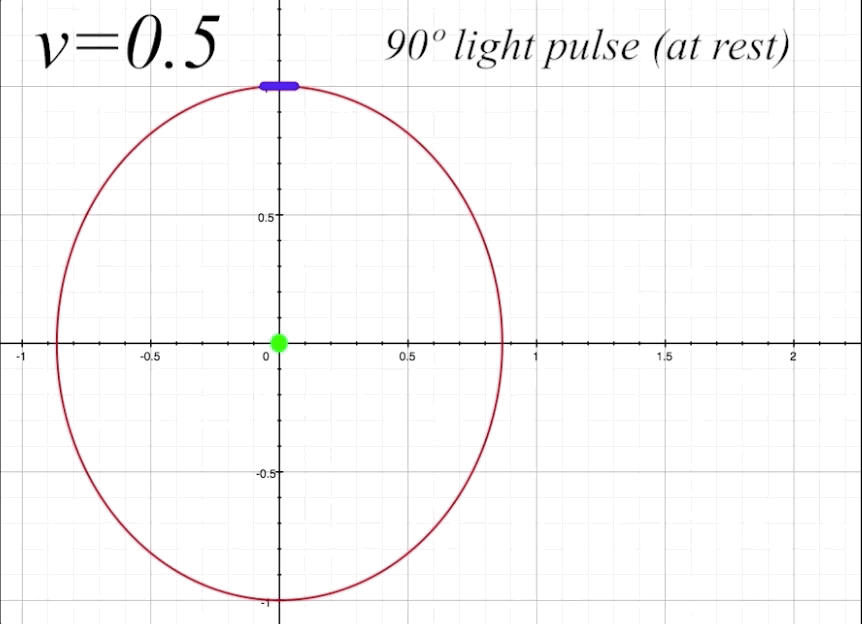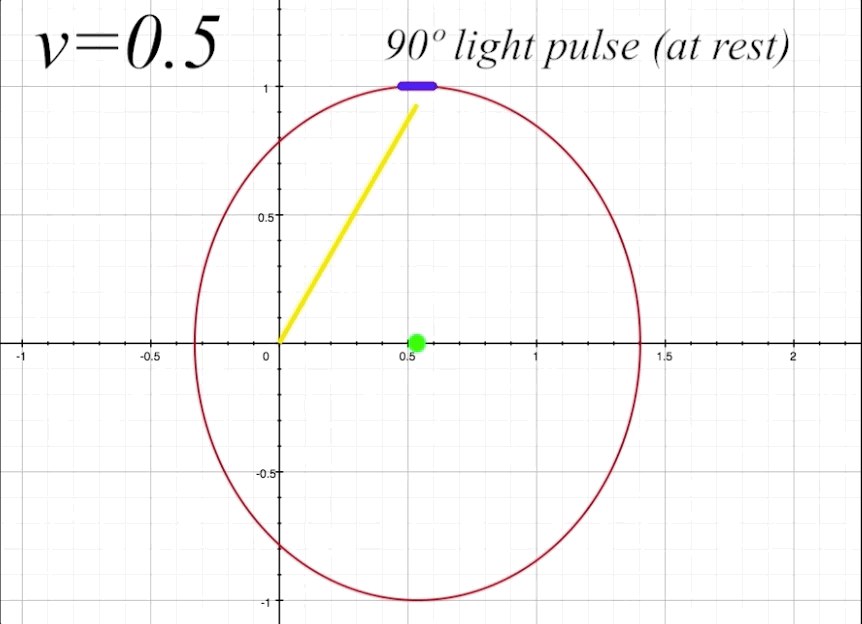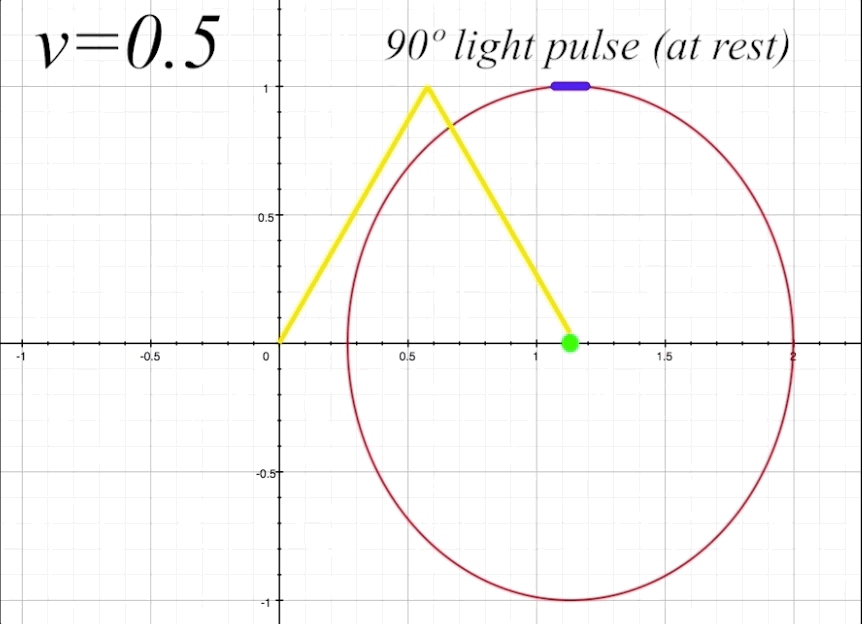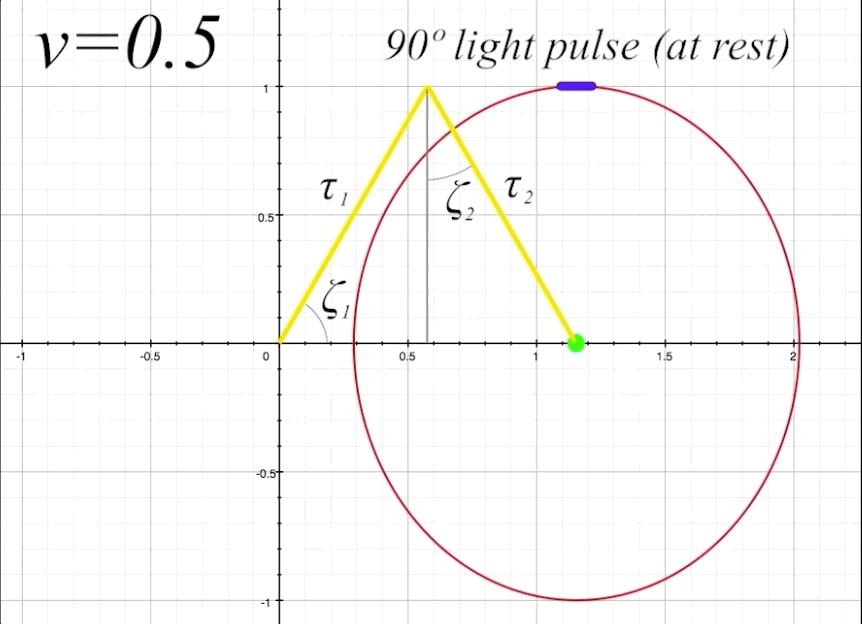
We will now prepare to calculate the proper time \(\tau_{1}\) that the light will take to travel to the mirror with the ship at \(v = 0.5\) and the light pulse rest angle \(\theta\) at 90º. Proper time is the elapsed time perceived by an outside observer of the light pulse as it travels from the center of the ship to the mirror. As we need to consider time dilation and length contration to calculate \(\tau,\) we will introduce the Lorentz factor \(\gamma\) into our equation. The Lorentz factor is represented by
\[\gamma = \frac{1}{\sqrt{1-v^2}}\]
And the formula to find \(\tau_{1}\) is
\[\tau_1 = \gamma(v\cos\theta + 1)\]
which is functioning as a Lorentz transformation. We will look more closely at our formula later, but for now when we plug in the angle values we find that the light pulse travels a distance of 1.1547 light-seconds to the mirror, and the same on the return path to the occupant. That is from our outside perspective frame of reference. The occupant, however, will always see the light pulse taking two seconds to return after reflecting from the mirror and back, regardless of the velocity of the ship, due to the combined effects of time dilation and length contraction in the occupant's frame of reference.
The return path of the reflected light pulse \(\tau_{2}\) can be calculated by one sign change within our formula:
\[\tau_2 = \gamma(\text{-}v\cos\theta + 1)\]
The formula that reveals the proper time \(\tau_2\) of the light pulse reflection does not indicate whether the angle of the light pulse is toward or away from the direction of ship's motion; in other words, \(\tau_2\) could describe a displacement of equivalent length that propagates either to the left or the right along the x-axis. Later when we need to know the specificity of the direction, we will introduce a way to produce this information. But now we are only concerned with the combined proper time of the light pulse by \(\tau_1\) and \(\tau_2,\) as perceived by an external observer.
\(\tau_1 + \tau_2 = 2.3094\;\text{sec.,}\) as perceived by an outside observer at rest for the time of the complete light path, from center of ship to the mirror and reflection back to ship's center. Now, the ship's occupant, moving at \(v = 0.5,\) experiences time dilation of \(\gamma,\) where \(\gamma = \frac{1}{\sqrt{1-v^2}}.\) At \(v = 0.5, \gamma = 1.1547,\) which means the ship's occupant is experiencing 1 second of proper time \(\tau\) as \(\frac{\Delta\tau}{\gamma.}\) Since the time \(\tau_1 + \tau_2 = 2.3094\) for the light pulse to travel both directions, as perceived by ourselves as outside oberservers, and since the occupant will experience the elapsed time light path as a change in proper time \(\Delta\tau\) divided by \(\gamma,\) we arrive at the occupant's perception of the elapsed time of the light path to be
\[\frac{\Delta\tau}{\gamma} = \frac{2.3094}{1.1547} = 2\text{ sec.}\]
which is precisely the value needed for both frames of reference to be Lorentz invariant, and for the occupant to always experience the same time for the light pulse to return regardless of velocity.
We can use the example above for a simple explanation of how reflection angles from the surface of a mirror are calculated. Since the mirror's surface is parallel to the direction of motion, there is no change in the mirror's angle due to length contraction, as we mentioned above. The law of reflection states that a light pulse arriving to a mirror, called the incident ray, will reflect from the mirror at the same angle that it arrived, but on the opposite side of a line called the surface normal. The surface normal is simply a line that is perpendicular to the mirror's surface. This will not hold true however, when the mirror is at any other angle \(\alpha\) in relation to the direction of motion except parallel or perpendicular to the direction of motion. Any other angle \(0º<\alpha<90º\) will result in a change in the laws of reflection from the perspective of an outside observer. But we will explore that phenomenon later, and first look at reflection and surface normal under 'normal' circumstances.
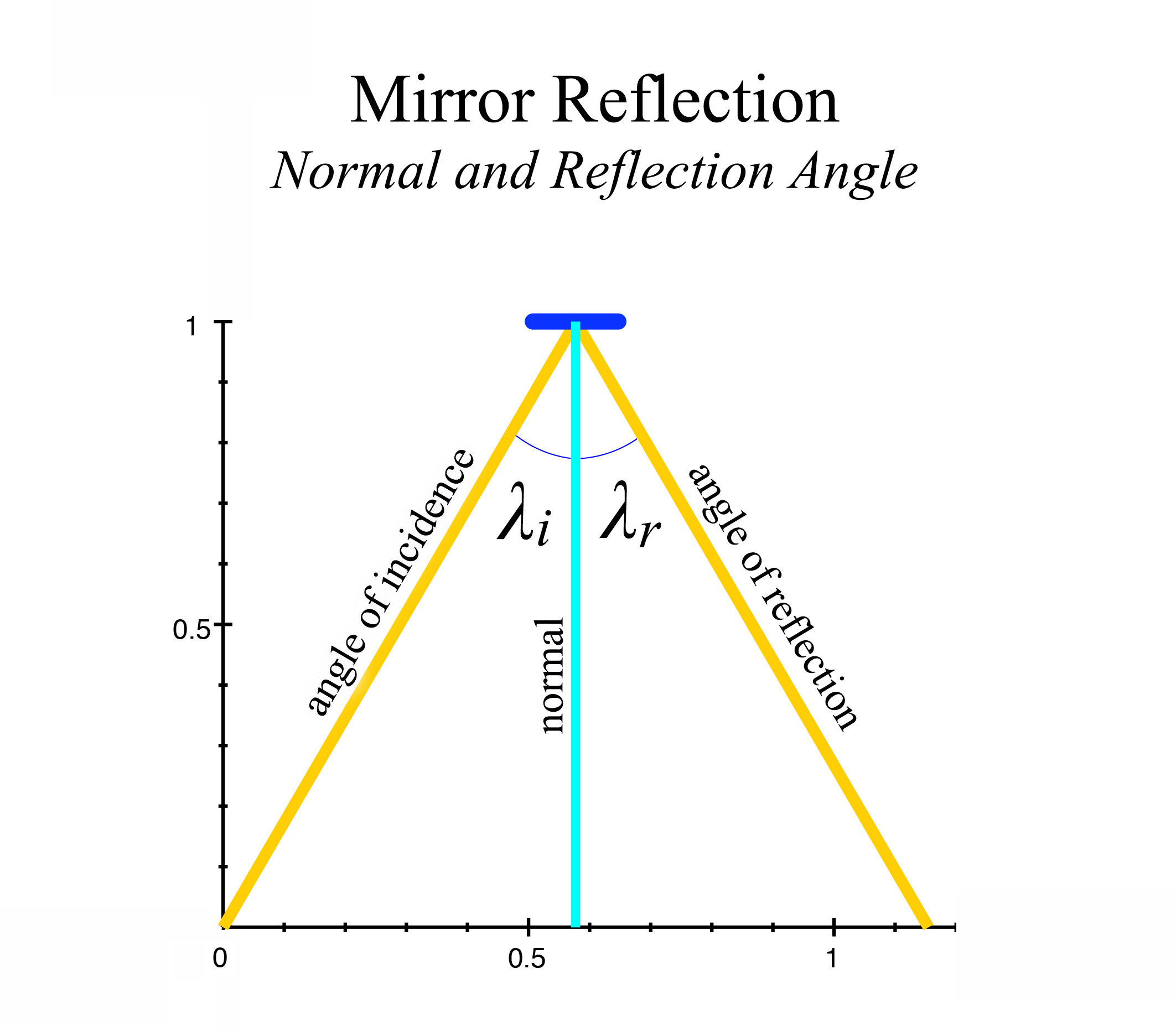
figure 3b, Mirror normal and angles of incidence and reflection
In figure 3b, we see that the mirror angle is at 0º in relation to the x-axis, and so would have a normal of 90º in relation to the mirror's surface angle. We consider the normal then to be at 0º to the y-axis. A light ray, called the angle of incidence (\(\lambda_i\)) striking the mirror's surface at an angle of 30º from the normal, will then have an angle of reflection (\(\lambda_r\)) off the mirror also at a 30º angle from the other side of the normal line. We see that \(\lambda_i = \lambda_r, \) and the surface normal bisects \(\lambda_i + \lambda_r\) in the center, giving an angle of reflection of equivalent size to the angle of incidence, in relation to the normal. This is the basic law of reflection. In the scenario presented in figure 3a, that law holds true from the perspectives of both the ship's occupant, and the outside observer. However, the law will require modification as we begin to employ other mirror angles in our examples.
Now let's look now at a more complex situation, where the light pulse rest angle \(\theta\) is neither perpendicular nor horizontal to the direction of motion of the ship. In figure 4, the light pulse angle \(\theta\) is 60º, and the mirror rest angle \(\alpha\) is at right angles to the light pulse, angling down at -30º. We'll start with the ship at rest, or \(v = 0\) and take a preparatory look at the details.
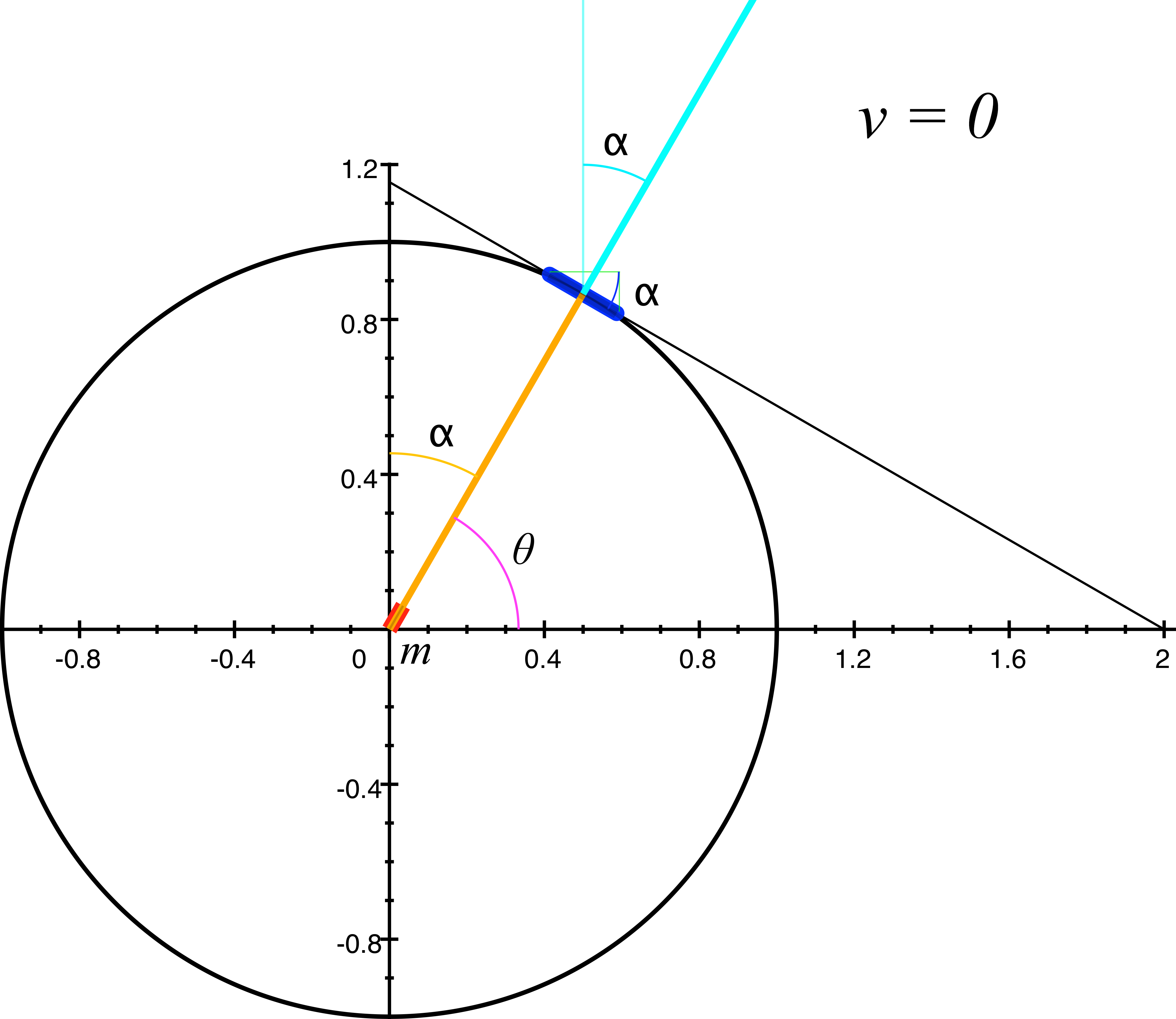
figure 4, ship at rest
At rest, as we observe in figure 4, the angle \(\alpha\) of the mirror is orthogonal to the angle \(\theta\) of the light pulse, or \(\alpha = \theta - 90º.\) And at rest, there is no funny business; from both an external observer's perspective (our perspective), and the spaceship occupant's perspective; the mirror remains at a right angle to the light pulse, time is not dilated for the occupant, and there is no length contraction of the ship and its contents. All seems right with the world.
But now let's give our ship a non-zero velocity, and send it along at half the speed of light, or \(v = 0.5.\) Let's first take a look at the relativistic length contraction that results when the ship is moving and see what that does to the angles of the mirror and the light pulse. The rest angle of our light pulse \(\theta\) at 60º and the rest angle of the mirror \(\alpha\) at -30º will change when length contraction occurs from the ship's velocity. As we mentioned above, to differentiate between the rest angles and the moving angles of the light pulse and the mirror, we will refer to the moving angle of the light pulse as \(\zeta,\) and the moving angle of the mirror as \(\beta.\) In figure 5 we see a still frame example of the ship moving at \(v = 0.5,\) and we notice that the length-contracted rest path of the light pulse is now represented by a dotted line. That is because when the ship is in motion, the light will not take that path, but will move forward at a lesser angle \(\zeta_1\) along with the motion of the ship. We also note that, due to length contraction, the apparent rest angle \(\theta\) of the light pulse has changed. We will label this contracted angle \(\sigma\), but unlike the light pulse rest angle \(\theta,\) we will define \(\sigma\) in relation to the y-axis instead of the x-axis. For now we won't worry about \(\sigma,\) but it will become essential when we calculate the altered reflection properties of the mirror. For now, figure 5 is only exhibiting the length contraction of the ship while in motion, and the consequential change in mirror angle from \(\alpha\) to \(\beta,\) and the change from \(\theta\) to \(\zeta_1\) of the light pulse.
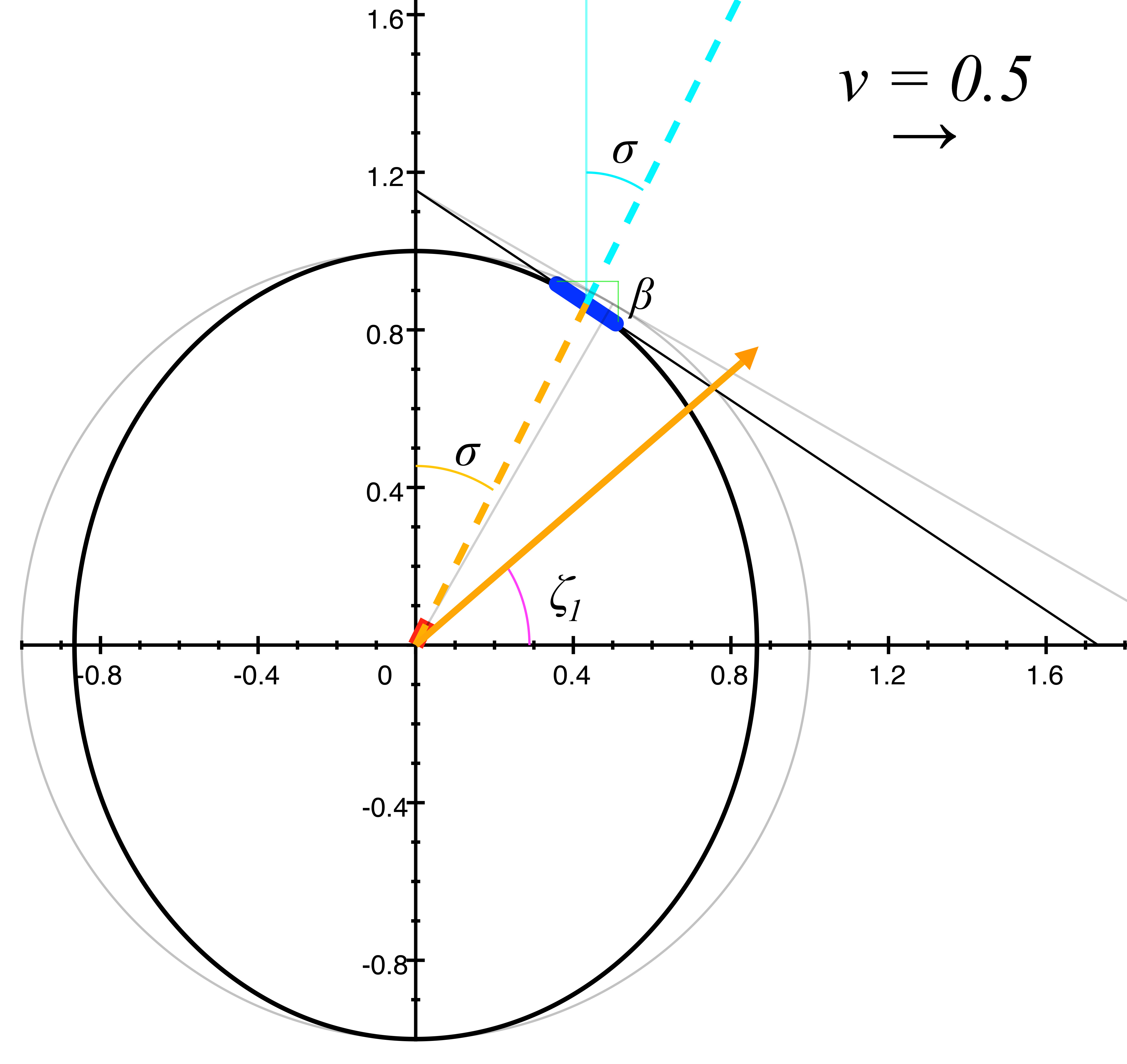
figure 5, light ship at v = 0.5, showing length contraction and change in angles
We note that when the ship is at rest (figure 4), both the mirror angle (in relation to the x-axis) and the light pulse emitter angle (in relation to the y-axis) are represented by the same value \(\alpha.\) When the ship is in motion however, this symmetry vanishes; the changes due to length contraction along the direction of motion of the ship gives us the discrete angle values \(\beta\) and \(\sigma\) respectively for the mirror and light emitter angles.
Let's find the mirror's length-contracted angle \(\beta.\) Length contraction is calculated by \(\sqrt{1 - v^2},\) and since the mirror is subject to length contraction within the ship, we can calculate the mirror's angle \(\beta\) after length contraction at any velocity by
\[\beta = \tan{^{-1}}\frac{\sin \alpha}{{\sqrt{1 - v^2}}(\cos \alpha)}\]
As we see, the formula for length contraction is only applied to the cosine of the mirror's angle \(\alpha,\) since the cosine lies on the x-axis, and length contraction only occurs in the direction of motion, which in our examples is along the x-axis. Therefore the sine of \(\alpha\) is not contracted. In figure 6 below, we show the ship at \(v = 0.5,\) and we can see that the angle \(\beta\) of the mirror at \(v = 0.5\) has steepened from its rest angle \(\alpha.\) When we plug in -30º for the mirror's rest angle \(\alpha\) and 0.5 for the value of \(v\), we arrive at the mirror's moving angle \(\beta\) as:
\[\beta = \tan{^{-1}}\frac{\sin(\text{-}30º)}{{\sqrt{1 - 0.5^2}}(\cos(\text{-}30º))}\]
or
\[\beta = \text{-}33.69º\]
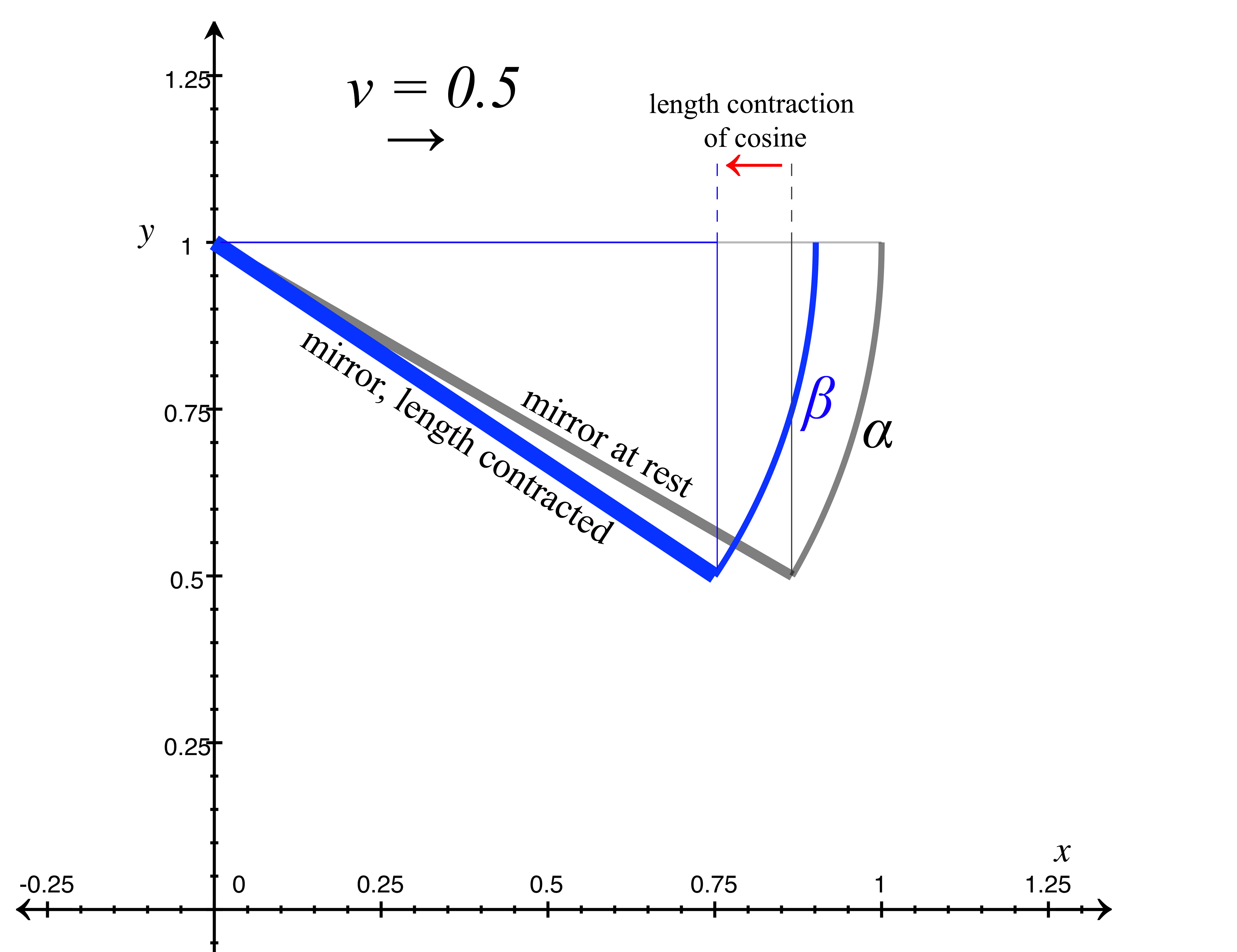
figure 6, ship at v=0.5 showing mirror length contraction and angle change
Since \(\alpha\) represents both the mirror angle at rest, and the angle of the light pulse emitter at rest, we now look at how the light pulse emitter's angle \(\alpha\) changes due to length contraction. As we see from the blue line in figure 7 below, it is now the sine that is along the direction of motion; unlike the mirror angle \(\alpha,\) which has the cosine along the direction of motion. That is because even though both angles are represented by \(\alpha,\) they are oriented at a 90º rotation from each other, and the angles are in relation to the x-axis and y-axis respectively. To find the new angle of the light pulse emitter \(\sigma,\) we will do the same type of calculation on angle \(\alpha\) that we did to arrive at \(\beta,\) but instead will apply the length contraction to sine \(\alpha,\) instead of the cosine.
\[\sigma = \tan{^{-1}}\frac{{\sqrt{1 - v^2}}(\sin \alpha)}{\cos \alpha}\]
which gives us the length contracted angle value of
\[\sigma = 26.565º\]
The specific notation for the two equations above for finding the length contracted values of the mirror angle and light emitter angle, illustrates clearly how the side of each right triangle that is along the axis of motion experiences length contraction, thus altering the consequent angle. However, we can also write these equations more simply as follows:
\[\beta = \tan{^{-1}}(\gamma\tan \alpha)\]
\[\text{and}\]
\[\sigma = \tan{^{-1}}\frac{\tan \alpha}{\gamma}\]
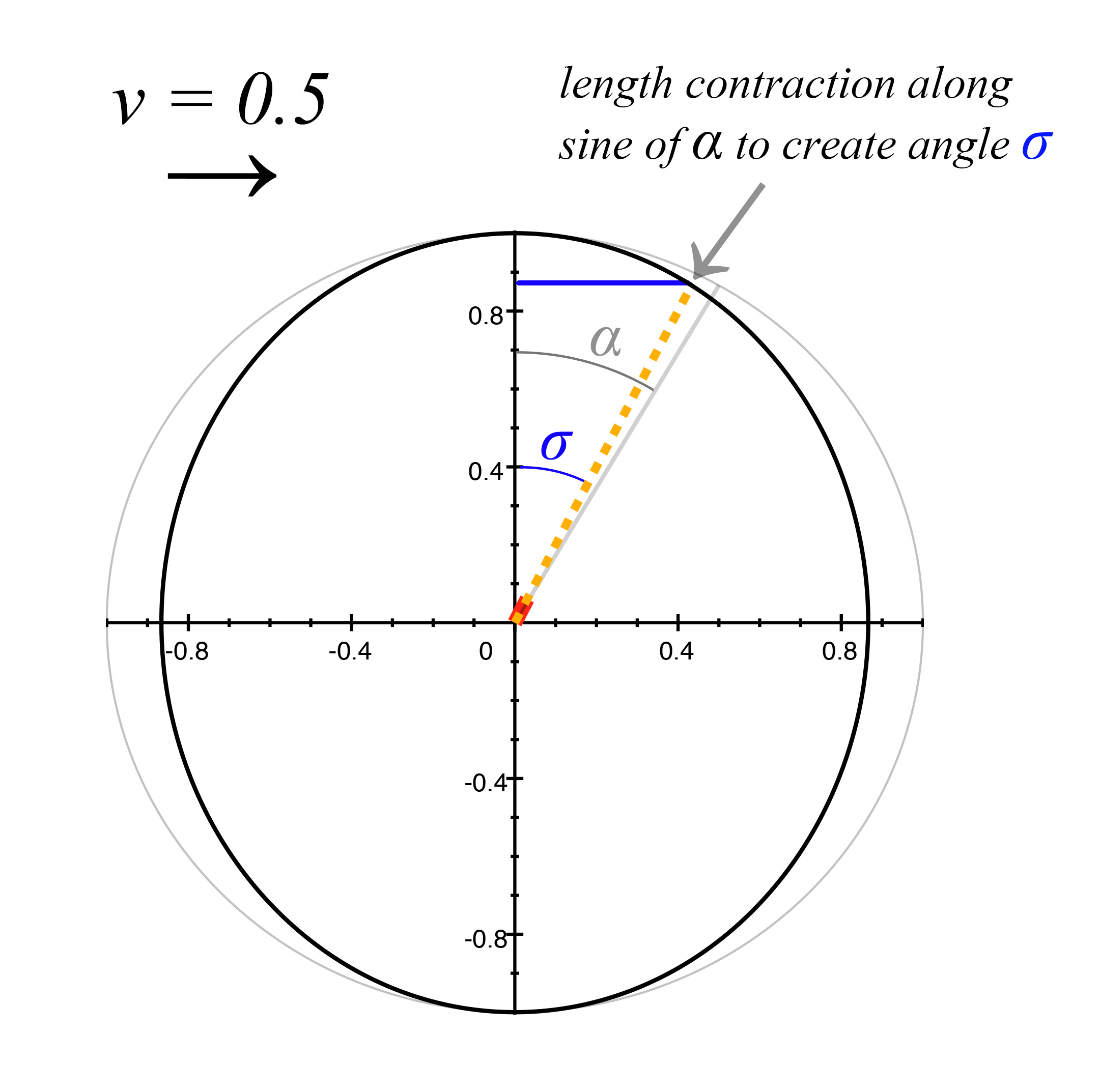
figure 7, ship at v=0.5 showing light pulse emitter angle change
The next thing to do is take a look at the full return path of the light pulse at \(v = 0.5\) and \(\theta = 60º,\) and examine the elements of the light trajectory and its reflection from the length-contracted mirror. Figure 8 below shows the complete round-trip trajectory of the light pulse departing from and returning to the occupant. Again, we are referring to the departing light pulse as \(\zeta_1,\) and the returning reflected light pulse as \(\zeta_2.\)
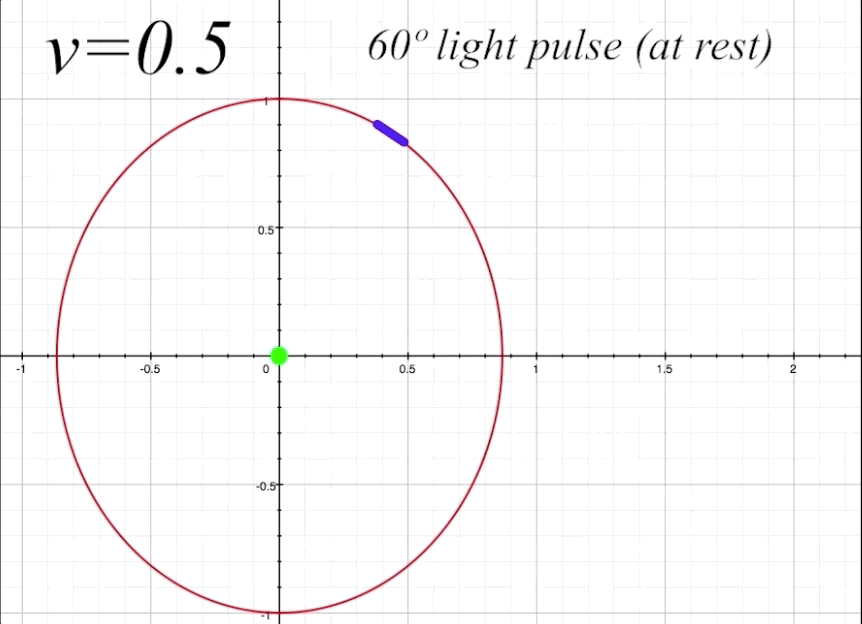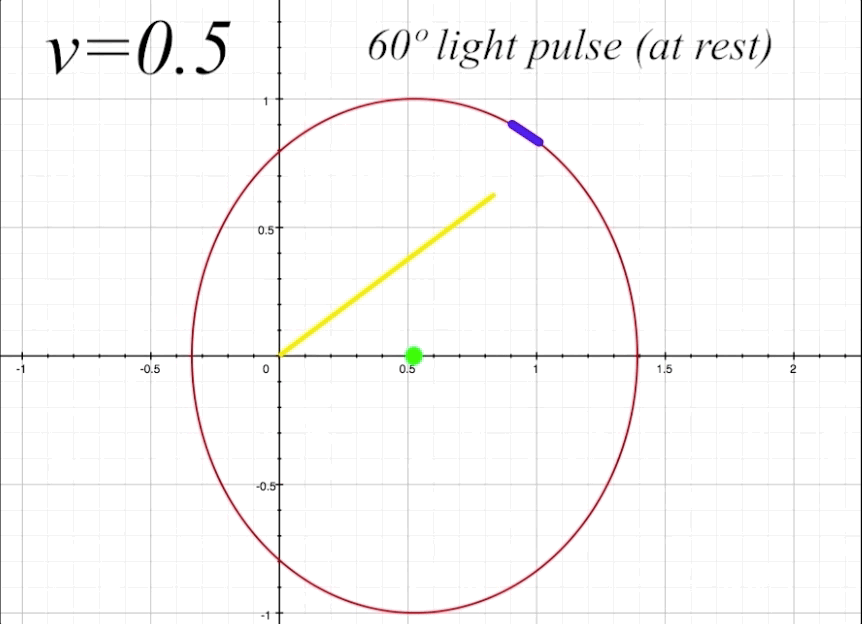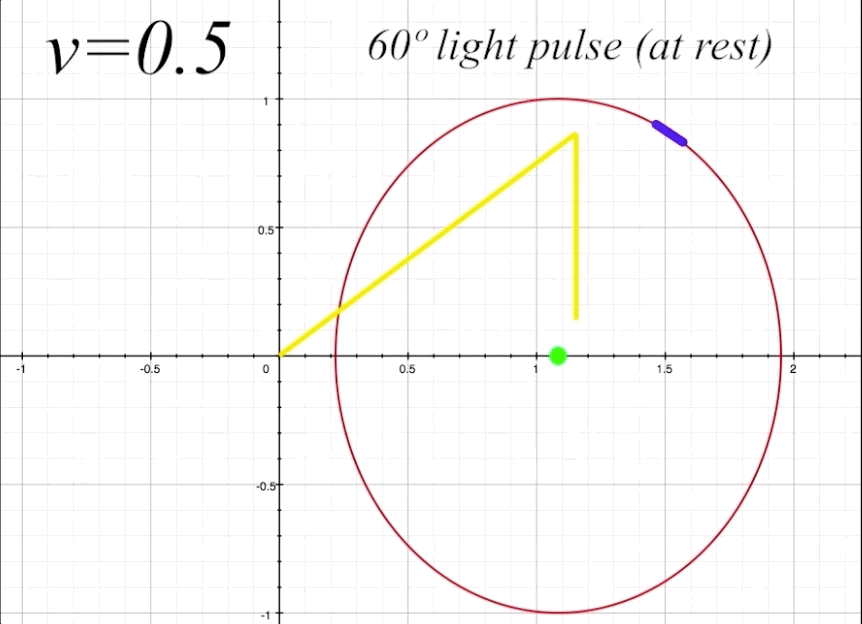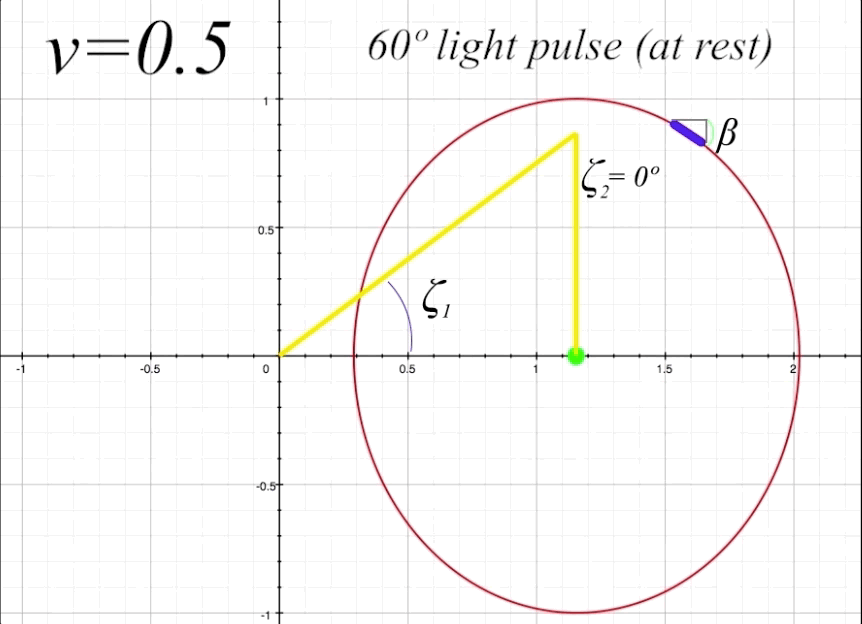
figure 8, ship at \(v = 0.5\) and \(\theta = 60º\)
We can now calculate the light angle \(\zeta_1\). Plugging in \(v = 0.5\) and \(\theta = π/3\) (because 60º \(= π/3\) radians) into our Lorentz transformation formula we find that
\[\tau_{1} = \gamma(v\cos\theta + 1) = 1.4434\; \text{sec.}\]
\(\tau_1\) constitutes the hypotenuse of a triangle with the opposite side being the sine of \(\theta\), which is 0.866. We can now find the angle \(\zeta_1\).
\[\zeta_1 = \sin{^{-1}}\biggl(\frac{\sin\theta}{\tau_1}\biggr) = 36.87º\]
We see that the proper time that we, as external observers, observe the light to take as it travels from the center of the ship to the mirror to be \(\tau_1 = 1.4434\). We also observe the angle \(\zeta_1\) of the light pulse to be 36.87º. Before we look at how things appear to the ship's occupant, let's complete the round trip of the light pulse, as it bounces back to the occupant at ship's center. We use the polarity modified Lorentz transformation to achieve the proper time \(\tau_2\) of the light's return trip from mirror to occupant:
\[\tau_2 = \gamma(\text{-}v\cos\theta + 1) = 0.866\; \text{sec.}\]
By the same process we used above, we can find the angle of the return path of the light pulse, as perceived by outside observers. However, we want to see \(\zeta_2\) in relation to the y-axis, unlike \(\zeta_1,\) which we need to see in relation to the x-axis. For this reason, when calculating the angle for \(\zeta_2,\) we will need to use the inverse cosine instead of the inverse sine to show its relationship to the y-axis:
\[\zeta_2 = \cos{^{-1}}\biggl(\frac{\sin\theta}{\tau_2}\biggr) = 0º\]
This is interesting, showing that the angle of the return light pulse here is straight down to the occupant, which makes sense when looking at the value of \(\tau_2\), since at a proper time value of 0.866 seconds, and vertical distance to travel along the y-axis of of \(\cos\theta =0.866\) (which is the vertical distance in this example between the mirror and the occupant), the only possible path for the light to take would be straight down the y-axis to intersect with the occupant, giving \(\zeta_2\) a value of 0º.
Now we will see how the mirror's surface normal no longer follows the law of reflection when the mirror is in motion, from the perspective of an outside observer. In figure 9 below, we see the mirror with angle \(\beta\) (in this example \(\beta = 33.6º),\) and the normal line as would be expressed by the law of reflection is represented by the dotted blue line. This line is at right angles to the mirror's surface, as the law of reflection states. However, the true normal is actually the purple line, with an angle \(\sigma\) in relation to the y-axis. \(\sigma = 26.565º,\) and this is clearly not at right angles to the mirror's moving angle \(\beta,\) or even the mirror's rest angle \(\alpha.\) We will call this true normal line the Dependent Normal, since its value \(\sigma\) depends on the length contraction of the mirror. Let's make sense of this.
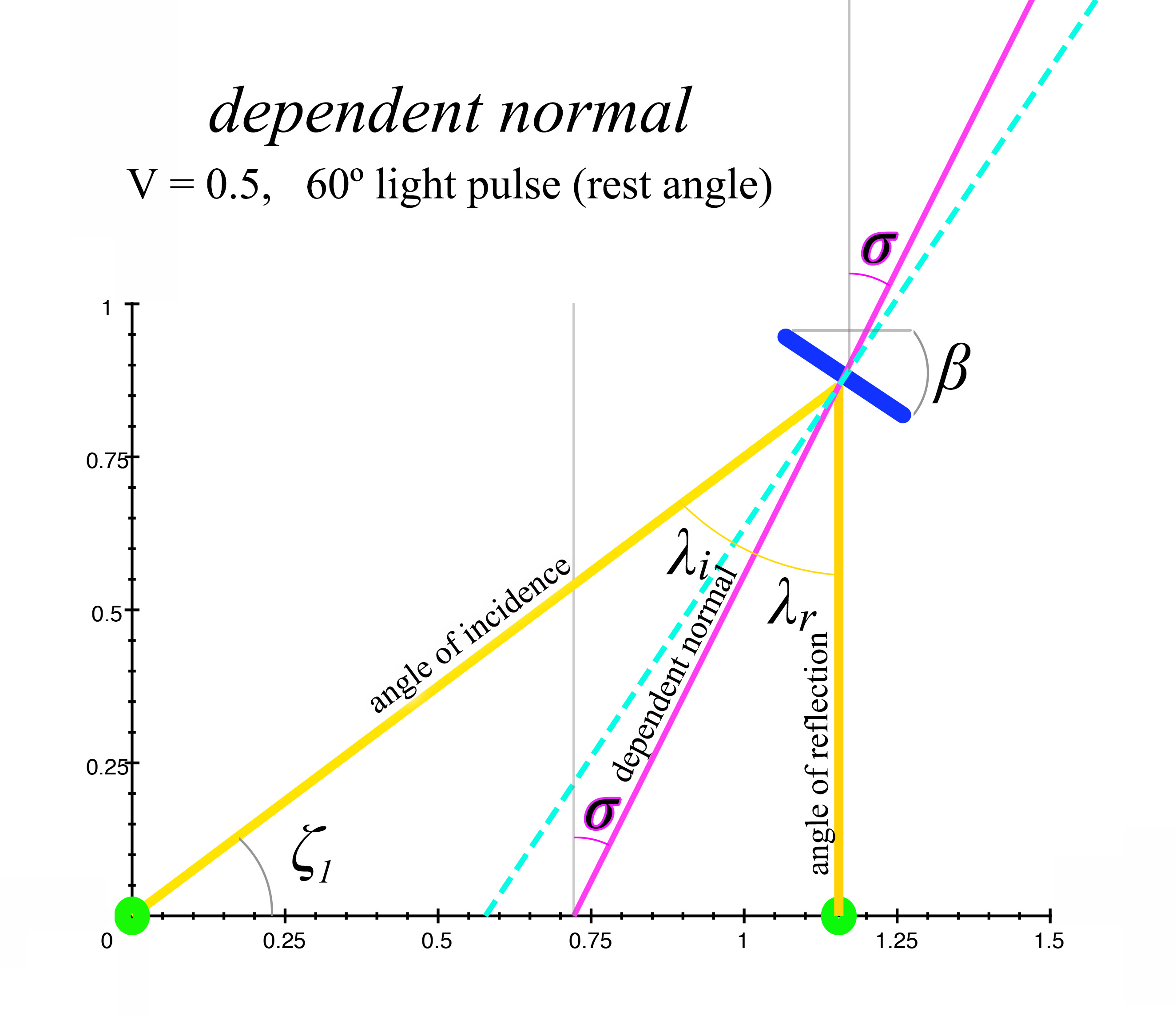
figure 9, dependent normal
It is important to realize that the observer in the same frame of reference as the mirror always experiences the normal as orthogonal to the mirror's surface; so no matter the velocity of the ship, the ship's occupant will always measure the normal line as orthogonal to the mirror's surface, thus satisfying the traditional law of reflection. However, from an outside observer's perspective, the normal is only seen as orthogonal to the mirror's surface when both frames of reference are at rest, or at the same velocity (which is equivalent in relativistic terms). If there is any difference in velocity between the two frames of reference, then the outside observer will perceive the angle \(\sigma\) of the mirror normal in the other frame of reference to be the dependent normal, which will never be orthogonal to the mirror's surface. At Newtonian velocities this would be very hard to measure, and the effect only becomes pronounced at relativistic velocities.
The dependent normal arises from the length contraction of the mirror's structure. Specifically, \(\sigma\) does not arise from the length contraction that changes the angle of the mirror's surface, but instead arises from the length contraction that is expressed along a line drawn through the mirror at right angles to the mirror's rest surface. This suggests that the properties of reflection are not determined by the angle of the mirror's surface, but from the length contraction of its internal structure that expresses along the traditional surface normal line, as it bisects the mirror.
Below we see the mirror's length contraction at \(v = 0.5.\) The mirror's rest structure is shown in light gray, and the length-contracted surface at \(v = 0.5\) is shown by the blue line. The purple segments show the length contraction along the line drawn through the mirror at right angles to the mirror's rest surface, and these segments express the true angle \(\sigma\) of the normal, the dependent normal, in relation to the length-contracted surface. We can clearly see that while the mirror is in motion, the purple segments are not at right angles to the blue line representing the mirror's surface.
We also note that all the consequent change in angle to the mirror's surface and to the orthogonal lines of the dependent normal occur solely from the contraction along the x-axis, which is along the direction of motion that the mirror is experiencing. We can see this illustrated by the horizontal lines across the mirror's structure, and we also see how the contraction in this dimension creates the internal properties from which the dependent normal angle \(\sigma \) arises.
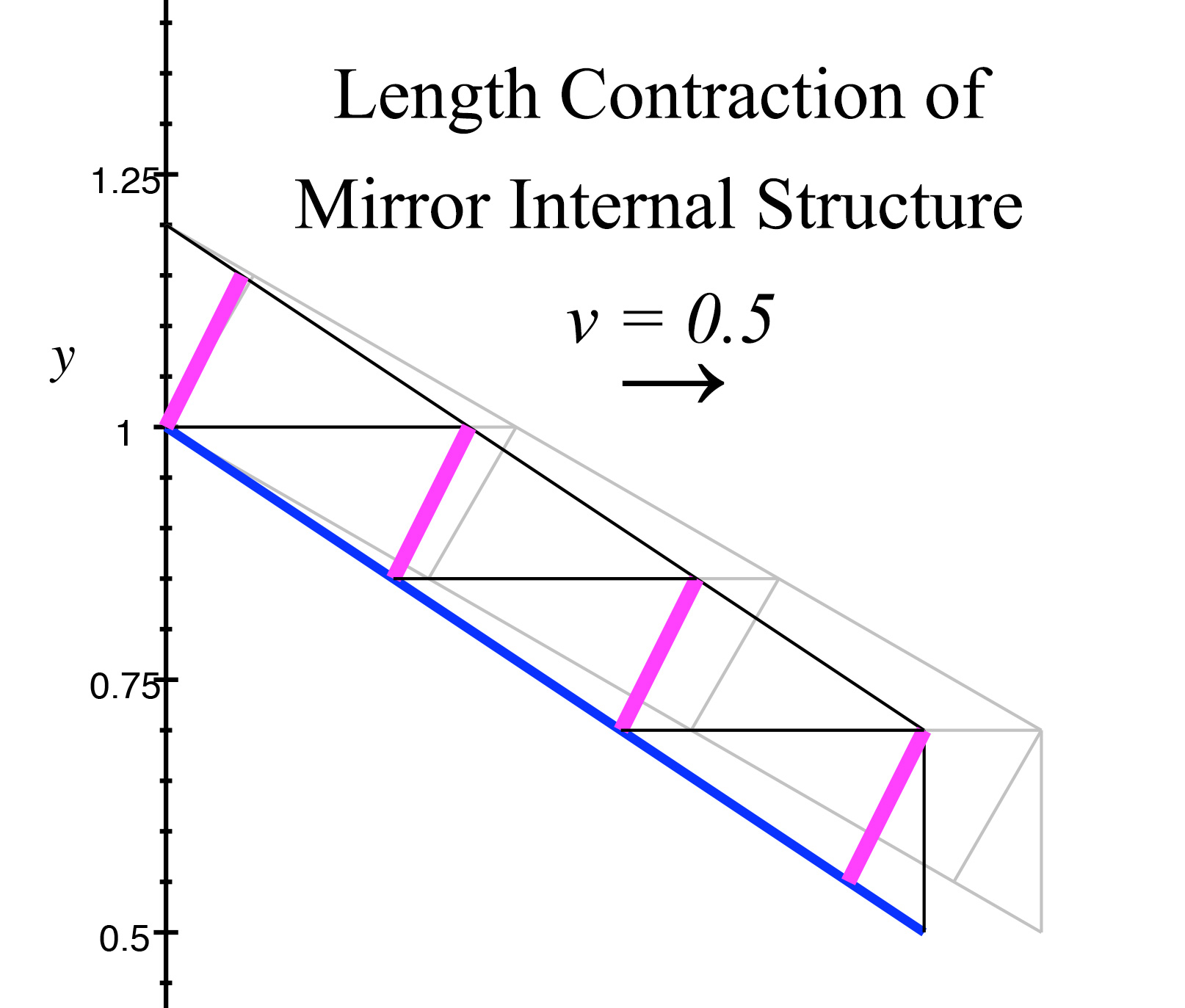
figure 10, length contraction of mirror internal structure and dependent normal
We can calculate \(\sigma\) in a number of ways. As a function of the length-contracted angle \(\beta\) of the mirror, we have
\[\sigma = \tan{^{-1}}\bigl(\tan\beta (1 - v^2)\bigr)\]
which can be derived from a formula using the rest angle \(\alpha\) of the mirror to calculate \(\sigma\):
\[\sigma = \tan{^{-1}}\biggl(\frac{1}{\gamma}\frac{\sin\alpha}{\cos\alpha}\biggr)\]
Ultimately, we can determine the value of \(\sigma\) as a relationship of the angles \(\zeta_1\) and \(\zeta_2\) of the light pulse, and \(\lambda:\)
\[\sigma = \lambda_i - \frac{(\frac{π}{2} - \zeta_1) + \zeta_2}{2}\]
And a formula for \(\lambda_i\) and \(\lambda_r\) is also derivable from \(\zeta_1\) and \(\zeta_2\) by choosing the absolute value of \(\zeta_2:\)
\[\lambda_i = \lambda_r = \frac{(\frac{π}{2} - \zeta_1) + |\zeta_2|}{2}\]
\(\lambda_i\) and \(\lambda_i\) always have equivalent values, because the angle of reflection equals the angle of incidence, in relation to the normal.
Now we will dig a little deeper, to explore a more complicated scenario for the return light pulse angle \(\zeta_2\). In our previous example with \(\theta = 60º,\) we were in the unique position of having the return light pulse angle \(\zeta_2 = 0º,\) which meant the light path moved straight down along the y-axis to the occupant, and there was no displacement along the x-axis of \(\zeta_2,\) in either a positive or negative direction. But if we change our setup to light pulse rest angle \(\theta = 45º\) and mirror rest angle \(\alpha = -45º,\) then the return light pulse angle \(\zeta_2\) will require more attention to produce the correct signed value of its x-axis displacement
First we will view figure 11 below showing the light path angles of \(\zeta_1\) and \(\zeta_2\).
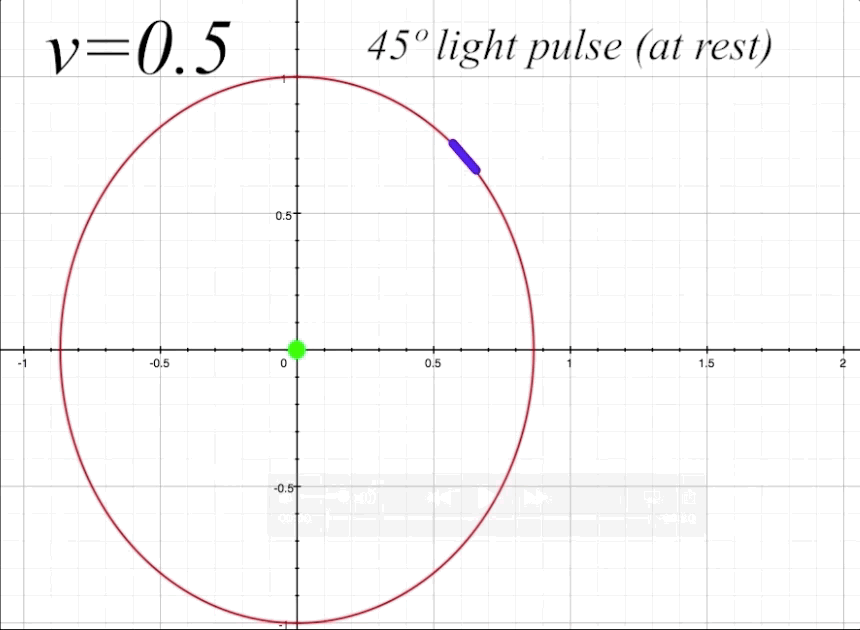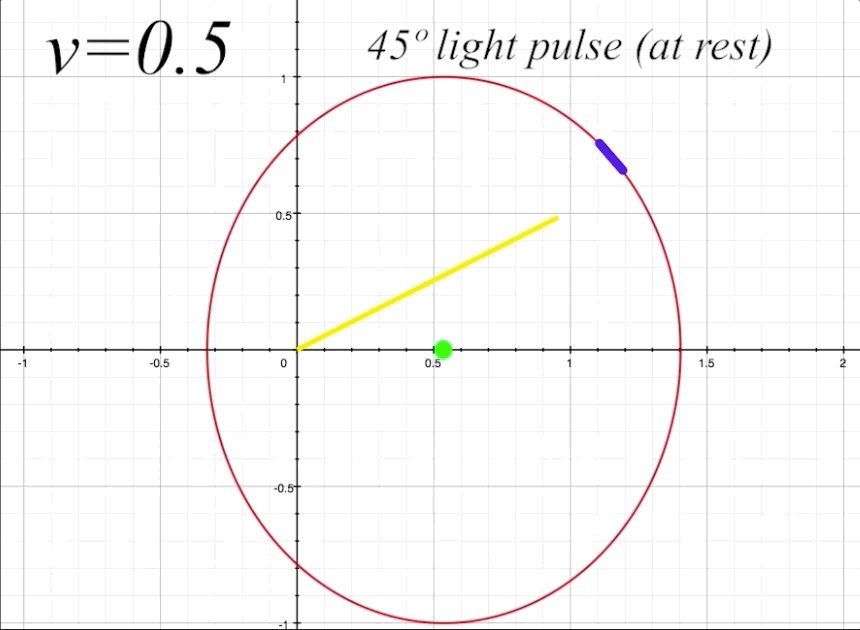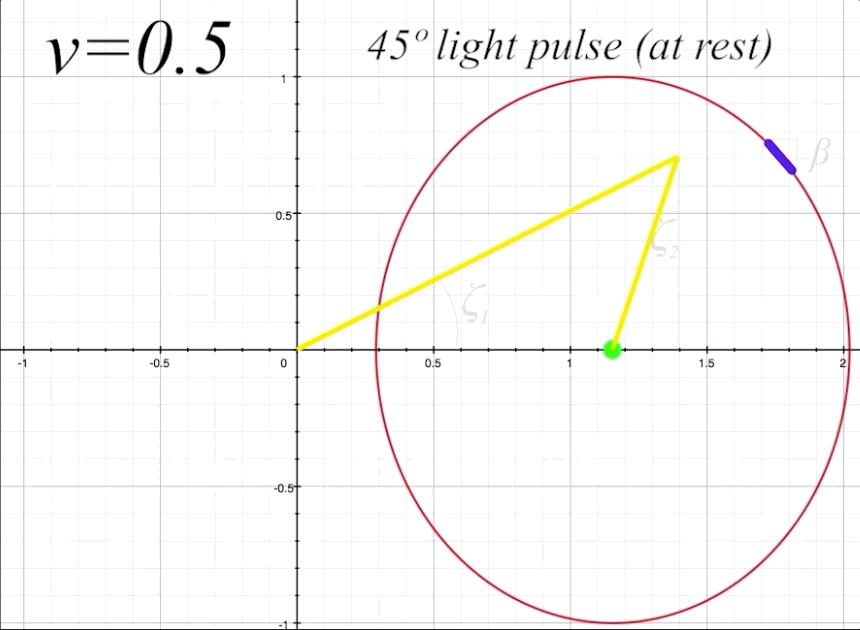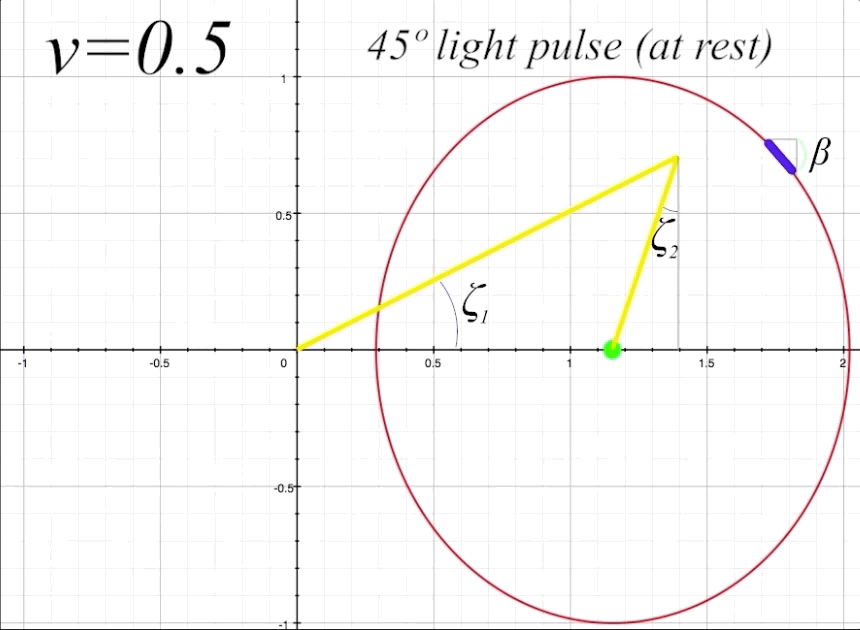
figure 11, ship at \(v = 0.5\) and \(\theta = 45º\)
As we see, the return path of the light pulse described by \(\zeta_2\) has a negative value along the x-axis. The problem is that our previous method of calculating these angles using the Lorentz transformation does not include information about the direction of displacement. For example, if we calculate
\[\tau_2 = \gamma(\text{-}v\cos\theta + 1) = 0.7465\]we find that it does give us the correct length and time \(\tau_2\) of the return light pulse, but the data indicating the direction of displacement is lost. As we see below in figure 12, there are two angles \(\zeta_2\) that can emerge from the Lorentz formula, only one of which is correct.
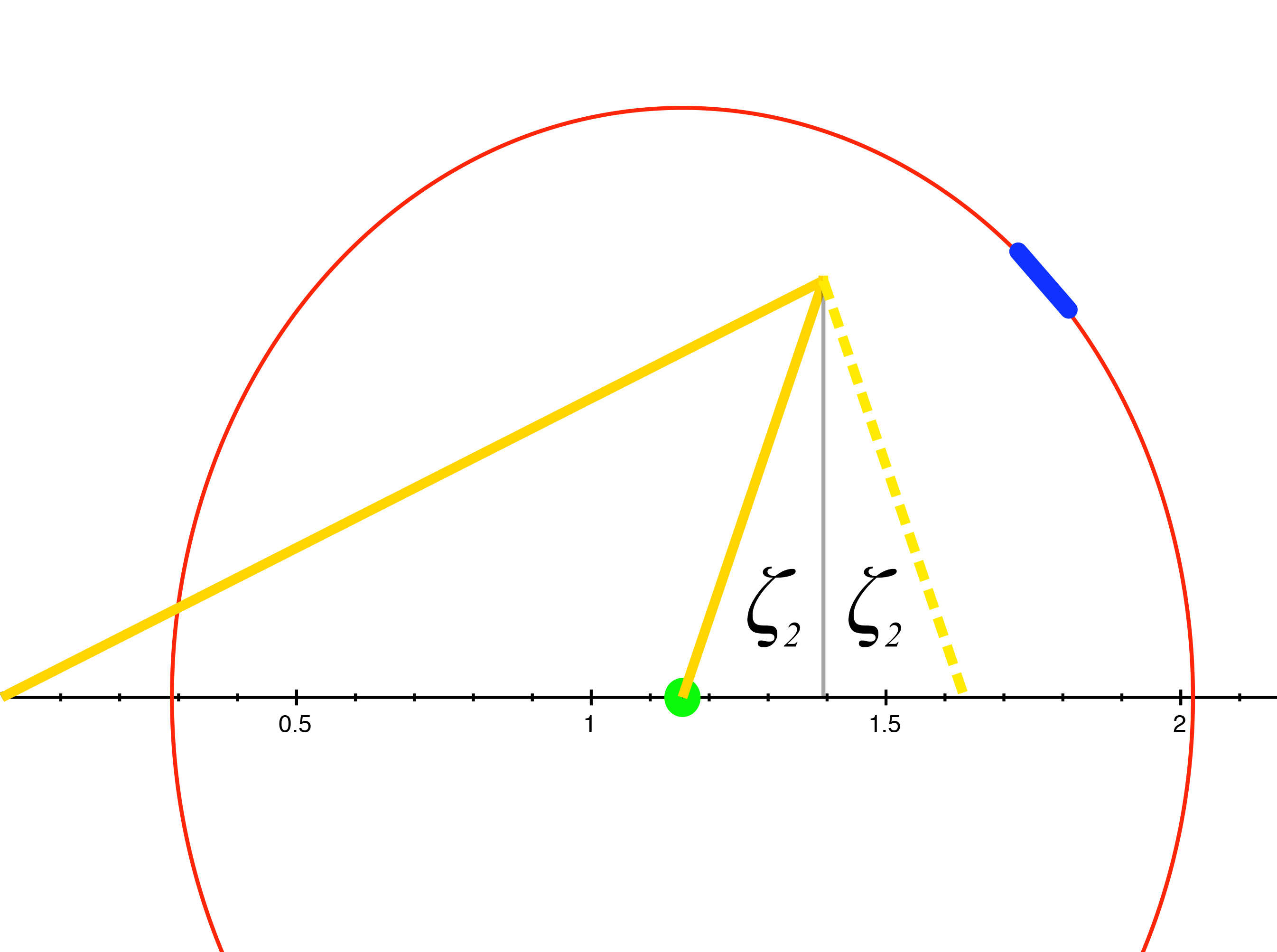
figure 12, two possibilities of return path of light pulse
It's clear that of the two possible angles for \(\zeta_2,\) only one can be correct, since only one possibility will allow the return light pulse to successfully intersect with the occupant. We can easily put in by hand the necessary information to determine which angle is correct and continue to use the Lorentz formula, since if \(\theta < \cos{^{-1}}v\) then \(\zeta_2\) will be negative. But instead, let's create a second-degree polynomial equation that will return signed displacement data for \(\zeta_2\) intact. In doing so we will have a clear and verifiable demonstration of the relationship between the movement of the light pulse and the position of the moving ship.
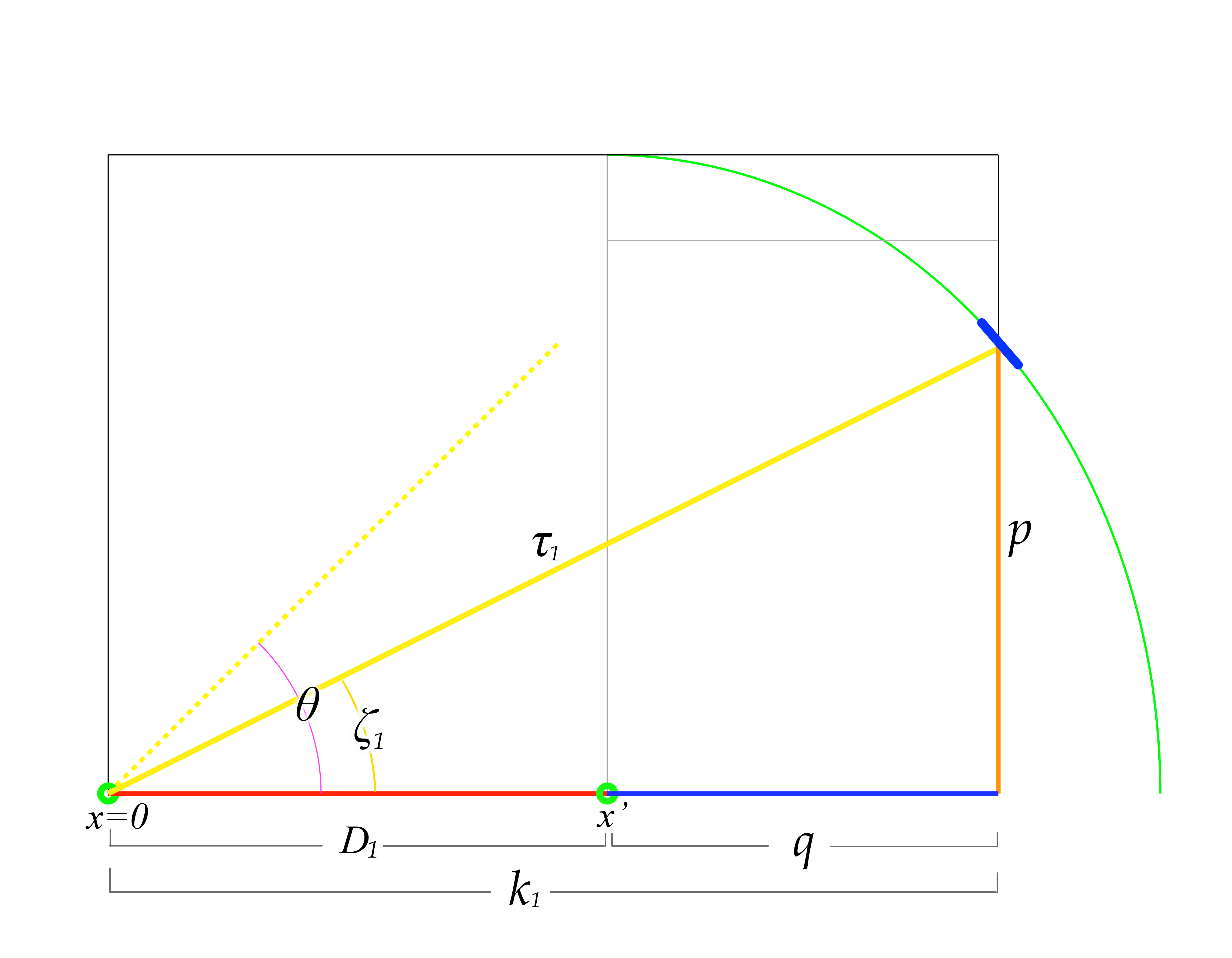
figure 13
In figure 13 above we have the necessary information that we can use to create our polynomial equation. In this figure, \(v = 0.5\) and the light pulse rest angle \(\theta\) is 45º. We note that for all values of \(v,\) \[p =\sin\theta\]
and
\[q = \frac{\cos\theta}{\gamma}\]
with \(q\) being the length-contracted distance along the x-axis between the ship's center and the mirror placement. In figure 13 we see \(q\) as the distance from \(x'\) to the point where the light pulse intersects the mirror; and of course \(x'\) represents the center of the ship where the occupant resides, and \(x'\) is the position the center of the ship will inhabit at the instance the light pulse strikes the mirror.
Let's begin with a statement that defines relationship of the light path to the distance the ship travels, which is
\[D_1 = v\tau_1\]
Studying figure 13 above demonstrates the correctness of this equation. At \(v = 0.5\) it is clear the distance \(D_1\) that the occupant will travel would have to be half the distance the light pulse traveles to the mirror, since the ship is going at half the speed of light. \(D_1\) represents the displacement along the x-axis of the ship's occupant, and \(D_1 = \Delta x.\) However, we must find only the one unique value \(\tau_1\) that describes the length of the light pulse at the exact instant that it strikes the mirror. This will also enable us to know the unique value of \(D_1\) that exists when the light pulse strikes the mirror. To find the exact values for \(D_1\) and \(\tau_1\) that will satisfy the parameters imposed by the ship's velocity, the angle of the light pulse, and the positioning of the mirror in the ship in relation to the occupant, we will first rewrite the equation to include the variable \(k_1,\) for which we can then solve. Since
\[D_1 = k_1 - q\]
and
\[\tau_1 = \sqrt{k_1^2 + p^2}\]
we can write \(D_1 = v\tau_1\) as
\[k_1 - q= v\sqrt{k_1^2 + p^2}\]
It is straightforward now to create a second degree polynomial that we can solve for \(k_1,\) from which we can generate the needed value of \(\tau_1.\)
\[k_1 - q = v\sqrt{k_1^2 + p^2}\]
\[(k_1 - q)^2 = v^2(k_1^2 + p^2)\]
\[k_1^2 - 2qk_1 + q^2 = v^2k_1^2 + v^2p^2\]
\[(v^2 - 1)k_1^2 + 2qk_1 + v^2p^2 - q^2 = 0\]
We have now reached a solvable quadratic equation, with numerical coefficients a, b and c shown in brackets:
\[\left[v^2 - 1\right]k_1^2 + \left[2q\right]k_1 + \left[v^2p^2 - q^2\right] = 0\]
Solving with the quadratic formula, we have
\[k_1 = \frac{-2q - \sqrt{(2q)^2 - 4(v^2 - 1)(v^2p^2 - q^2)}}{ 2(v^2 - 1)} = 1.3939\]
From this we now know that \(\tau_1 = 1.56295\) and \(D_1 = 0.7815,\) when \(\theta = 45º\) and \(v = 0.5.\)
We can also easily find the value of \(\zeta_1\) since we know the value of \(k_1,\) since \(\zeta_1\) would be the inverse tangent of \(p/k_1,\) or
\[\zeta_1 = \tan{^{-1}}\Biggl(\frac{p}{\frac{-2q - \sqrt{(2q)^2 - 4(v^2 - 1)(v^2p^2 - q^2)}}{ 2(v^2 - 1)}}\Biggr) = 26.9º\]
As illustrated in figure 12, there are two possible light paths for the reflected light pulse from the mirror, only one of which will arrive successfully to the ship's occupant. The information needed is whether the displacement along the x-axis of the trajectory of the reflecting light pulse \(\zeta_2\) is postive or negative; and our earlier Lorentz formula does not include this information and returns only the absolute value of the proper time of the light path \(\tau_2.\) However, with a modification of the quadratic expression above, the signed displacement along the x-axis will be supplied. We reverse the sign after the first term, as always in a quadratic formula when finding the second solution; but we must also reverse the polarity of the entire formula. Why do we need to reverse the polarity of the entire formula? The answer is an interesting puzzle to solve, and I will leave you the pleasure of figuring it out, if you wish. With both these polarity changes in place, the signed value for the x-axis displacement of the reflected light pulse can then be then returned as follows:
\[k_2 = -\frac{-2q + \sqrt{(2q)^2 - 4(v^2 - 1)(v^2p^2 - q^2)}}{ 2(v^2 - 1)} = -0.2391\]
It is interesting to note that \(k_1 + k_2 = \gamma\) for not only this instance, but for all possible values of \(\theta\) from 0 to 90º.
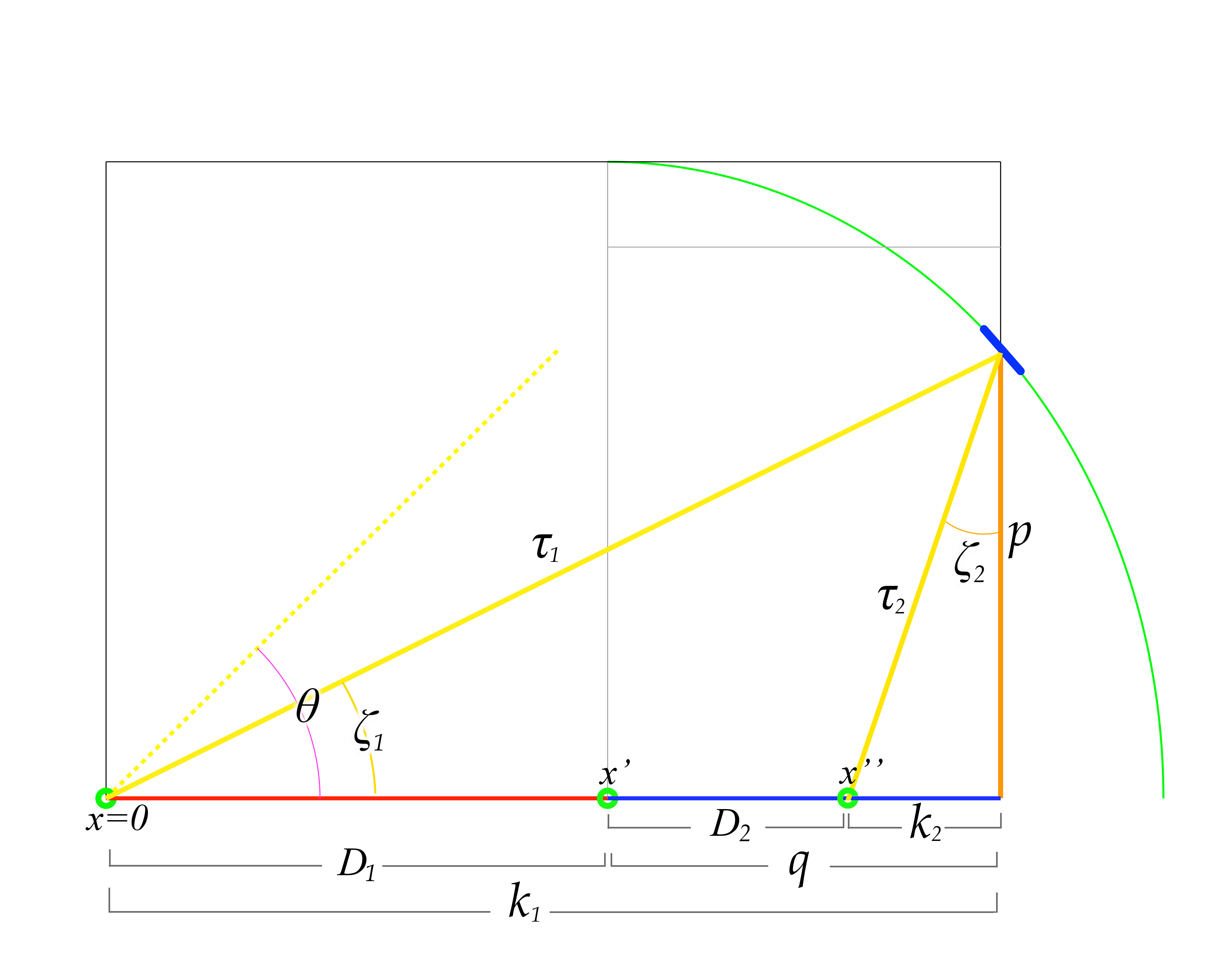
figure 14
As we see in figure 14, clearly the reflected light pulse is moving backwards against the motion of the ship to intersect with the ship's occupant at \(x'',\) with a distance of \(-k_2\) along the x-axis. We now have access to the true angle for \(\zeta_2,\) which would be
\[\zeta_2 = \tan{^{-1}}\frac{k_2}{p} = -18.68º\]
Which gives us the proper direction of the angle in relation to the y-axis.
Similarly, the value for \(\tau_2\) of the distance and time of the reflected light pulse is now available, as
\[\tau_2 = \sqrt{k_2^2 + p^2} = 0.7465\]
And so we have found the methods to solve the trajectories, distances and times of light pulse travel and reflection for any velocity and mirror placement within the parameters imposed by our model; and explored the necessary correction to the law of reflection by observing from an external frame of reference the anomalous reflection angles of a moving mirror. We have calculated the properties of a modified surface normal called the dependent normal that allows for an understandable manner of reflection for mirrors in motion, and we have shown how the dependent normal arises naturally from the length contraction of the internal structure of a moving mirror.