The answer to this thought experiment is a little more complicated than it might at first seem. Of course, the initial reaction of most people is that you would float up in the air, or go flying off into space. But the trajectory of our departure from the earth is a bit more interesting.
However, since we would clearly die of cold and hypoxia if we got high enough above the earth, let’s not allow our fear of mortality to keep us from this imaginative journey. So, we will allow ourselves the luxury of a science-fiction device no larger than an iPhone, that when switched on, surrounds us in a field that renders us unaffected by gravity, supplies us with breathable air, and also keeps us warm as we finally ascend tangentially into space. We’ll call our little device Grav-B-Gone.
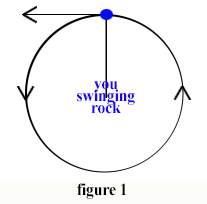
Have you ever swung a rock tied to a rope around your head? Me neither. But if you did, and let go, the rock does not fly straight out away from you, but at a right angle to the extension of the rope, along a tangent of the circle the rock is describing, in the direction of the swing.
Much like that rock, you are standing on the earth’s surface and moving quite fast as it rotates around its axis. In fact, if you are standing in Singapore (or anywhere else very near the equator), you are zipping along at about 1674 kilometers per hour. So if gravity no longer has any effect on you, you will continue to move at that speed, though now in a straight line, and not following the curve of the earth.
How do we figure out the speed we are moving on the surface of the earth from its rotation? We know that the radius of the earth at the equator (Re) is about 6,378 km, so to find the circumference of earth (Ce):
or Ce = approximately 40,074 km. Now we just divide Ce by the hours in a day to get the kilometers per hour we are moving. But, we can’t use a solar day because the earth is also orbiting the sun and changing its angle along the orbit a little bit each day, which gives us a false perspective about how much time a true full rotation of the earth really takes; so instead we use the sidereal day for our calculations. The earth’s sidereal day Sd = 23.934472 hours, and is based on earth’s rotation in relation to the positions of the stars. So we have
So this is pretty fast. And like the whirling rock on a string that is let go, you will also move in a straight line, going parallel to the earth’s surface, at the same speed that the earth is rotating. So initially, except for feeling weightless, it will seem that nothing much is happening for a short time.
A couple of caveats - we will not be taking into consideration any atmospheric influence in our trajectory. No gusts of wind, prevailing easterlies, westerlies, jet streams or bird collisions will we allow to alter our path. We are only concerned with the trajectory we will take in relation to the movement of the earth. We will later have to also consider the change in the earth’s direction as it orbits around the sun, and also the motion of the earth as part of the earth-moon system, and where that will put the earth’s position in relation to us as we move in our straight line out into space. These are the parameters we will consider in our thought experiment.
But first, let’s trace the path we will take caused by the earth’s rotation alone, and find out how to calculate that. Let’s first choose a place very close to the equator, so our first gravity-free journey will begin in Singapore, in the Gardens by the Bay.
We strap on our Grav-B-Gone and turn it on. After one second, we rise only about 1.7 centimeters off the ground straight up, and we could easily hold on to something to stop our ascent, but we don’t want to. By five seconds you have risen 42 centimeters off the ground. We have to remember that you aren’t really rising at all. You are actually going in a straight line in a tangent to the 0º latitude line of the earth upon which you were standing, and the earth’s curvature is actually receding away from you. By thirty seconds you would be a good 15 meters in the air, and after a minute a good 60 meters above the earth. You seem to be accelerating upward, but you are still describing a straight tangent line.
After five minutes you are now 1.5 kilometers high, looking far down on your point of departure, and an hour’s journey finds you 216 kilometers in altitude. Fortunately, your Gav-B-Gone is now providing you warmth and oxygen, and protecting you from space, because you are now out of the atmosphere. You also notice that your point of departure is now not directly beneath you. It is not the closest point on earth to you any longer, but is east of the point straight down. By six hours, you are an incredible 5,521 km above the earth, and your point of departure has begun an eastward migration and is now far, far to the east. You have traveled 10,000 km from your point of departure along the tangent line from the earth. But we have not yet included the additional motions of the earth which will result in different values - we'll introduce them later. But first a word about the choices made for our coordinate system.
Usually our frame of reference is the earth, with our coordinate system sticking like glue to the earth along its path through space. But I’ve chosen to have our frame of reference move at ≈ 30 km/sec linearly along the negative x axis.
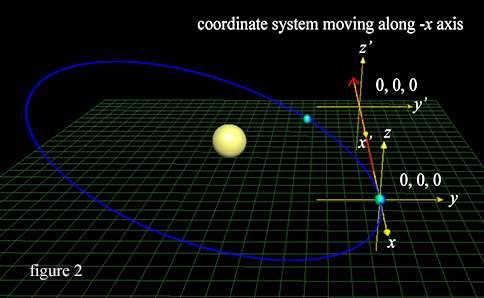
This is the speed of the earth’s orbit around the sun, and at our moment of departure from the equator, the zero points of our coordinate system will continue to move along the negative x axis at this velocity, along the tangent to the earth’s solar orbit. By so doing, we can easily illustrate the motions described by the earth from its orbital curve around the sun, and from the earth/moon gravitational interaction. Also, since our trajectory as we depart from the earth is solely along the positive x axis, it is easy to graph our journey.
Before we begin to work out the calculations, a few details about our frame of reference. We have set our three dimensional cartesian coordinate system so that a unit of 1 on the x, y and z axes represents the earth’s radius Re, or 6378 km. By keeping the units at value 1, the earth then has a radius of 1 in the coordinate system, allowing us to use trigonometric functions with all angles in radians. The equator lies exactly along the x-y plane at the moment of departure.
I have chosen to have the earth’s center starting position at x, y, z = 0, 0, 0. That means we will depart from 0, -1, 0 on our gravity-free trajectory, since we are at the surface of the earth, and the radius as we mentioned above will be at value 1. The earth will orbit counterclockwise from this position, heading into negative x and negative y values as it curves in its orbit around the sun. The earth’s orbital trajectory will also incline along the angle of ecliptic α = 23.5º along the positive z axis, reaching its highest z value 180º from its starting point at 0, 0, 0. We can see this above in figure 2.
We will depart on our journey at high noon from the equator, and we will naturally be moving at a composite of several speeds that the earth’s motions will impart to us, including earth’s rotation, the movement of the earth from the moon’s gravitation, and the tangent velocity of the earth’s solar orbit. Of all these, the one we can cancel out is the solar orbit velocity. Since both we and the earth are traveling at this same velocity at the moment of our departure, we can have the 0, 0, 0 point of our coordinate system also travel at the same velocity along the negative x axis. This effectively cancels out the velocity of the earth’s solar orbit as it applies to us and the earth at our moment of departure. Of course, the earth will immediately begin to curve into the negative y and positive z axes due to its orbital path, changing its position in the coordinate system, but we will take a look at that later.
We have also set our coordinate system so that the rotation of earth occurs exactly along the x-y plane. Since the ecliptic angle α = 23.5º, this means that the location of the sun is at an inclination of 23.5º along the z axis. Since the sun is 149.6e6 km from earth, and each unit in our coordinate system is Re, then the sun would be 149.6e6 / Re, or 23,481 units away from earth. This would be an hypotenuse at a 23.5º ecliptic angle from the earth’s starting position of 0, 0, 0. So, we will find the sun’s z coordinate by sin(α) * 23,481, or z = 9363, and the sun’s negative y coordinate by cos(α) * 23,481, or y = -21,533, with the earth’s center being at 0, 0, 0 at our journey’s inception.
We will use sidereal periods for both the rotation of the earth, the lunar month and solar year as well, because each full rotation of the earth will be in respect to the coordinate system and the fixed stars, and not in relation to the sun.
So, back to our trajectory. At high noon we left the surface of the earth at the equator, at x, y, z coordinates 0,-1, 0 (-1 on the y axis because, each unit of 1 represents Re, the radius of the earth. So at the moment of departure -1 is Re from the earth’s center at 0, 0, 0, putting us on the earth’s surface at y = -1). We can calculate the distance of our journey due to the velocity imparted to us by the earth’s rotation alone, along our straight tangent line by
Where
H = hours of journey
Vr = rotational speed at equator (1674.4 km/hr)
L = latitude of departure point
Since our latitude L = 0 at the equator, and cos (L) = 1, then we have Vr * 1, which would be 1674.4 km at one hour journey, or H = 1. By six hours we would have traveled 10,046 km along our tangent line, which we will call line "a", from the earth’s rotational velocity alone. We need to divide by Re to make our numbers usable for the trigonometry that will be needed.
However, none of this is yet the truth. We have not included the movement of the earth caused by the gravitational interaction with the moon, nor have we calculated the change in position of the earth along the curve of its solar orbit. We must include these two parameters to get a better approximation of our position.
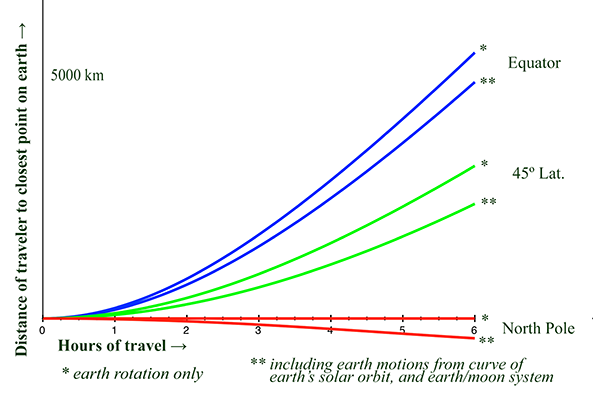
Let's take a look at departures from three different locations on earth: From the equator, which we have begun exploring, from 45º latitude (which we will illustrate at the end in our departure from Michigan), and from 0º latitude at the north pole. As we can see by the following graph in figure 3, our distance from the earth in each depature scenario is significantly different when we take into account the motion of the earth due to the sun and the moon. These extra motions move the earth toward us somewhat as we move on our trajectory, reducing the distance we are away from the earth. In fact, we see that after our departure from the north pole, we are actually calculated to be below the earth's surface due to these extra movements of the earth.
We will look at the movement of the earth in our coordinate system caused by the earth’s solar orbit. As we said above, our frame of reference is moving along the x axis at the speed of earth’s solar orbit. Initially the earth seems motionless in the frame since the velocities are the same. But rapidly the earth begins to change position along the x, y and z coordinates, caused by the curve of the earth’s solar orbit. Since this orbit is inclined at 23.5º in our coordinate system, in which the circle of 0º latitude demarcates the x-y plane, the earth will be seen to incline along the z axis and decline along the y axis as the earth orbits the sun. But let’s look first at how the earth will move along the x axis.
As the earth moves counterclockwise along its solar orbit, our R3 coordinate system moves along the negative x axis at the speed of the orbit. The earth and our coordinate system begin to diverge immediately as the earth curves away from the x axis. We can find the orbital angle ζ for any hour length H of earth’s orbit from the beginning of our journey with the equation
Where Y is the number of days in a sidereal year, or 356.25636 days.
As the earth curves away from the x axis, this means it will travel less distance than the moving coordinate system, and this will make the earth begin to move in a positive direction along the x axis. The change in x, or Δx of the earth’s x coordinate for any value H can be stated as
Where
Rb = radius of earth's solar orbit
Re = radius of earth
We can illustrate this with the following (figure 4), where we see the apparent motion of the earth moving in a positive x, negative y and positive z direction.
The term Rb/Re is needed to translate the results of ζ - sinζ to the correct x value for plotting in our coordinate system, where the radius of earth is represented by a value of 1. Rb is the radius of the solar orbit in kilometers, or 149.6e6, and when we divide Rb by the radius of the earth Re in kilometers, we have
Which, when multiplied by ζ - sinζ, gives us the x value we need for plotting within our R3 coordinate system.
To find the y coordinate value of earth for any value H due to solar orbit, we can use the equation
Where α = 23.5º, the angle of ecliptic
Since the angle ζ would be 180º after half a year, this would be the farthest extension of earth’s solar orbit along the negative y axis. Cosine of 180º = -1, so 1 - cos(ζ) = 2, the trigonometric diameter of the solar orbit. Now, since the solar orbit must incline by the angle of ecliptic α as it proceeds, we multiply (1 - cosζ ) * cosα to find the adjusted -y value due to the orbit’s ecliptic angle. And again we multiply -cosα(1 - cosζ ) by Rb/Re to find the correct y value for plotting in our coordinate system.
And finally for the z axis value, we follow the same procedure as for the y value above, the only differences being we use sine α instead of cosine α, and take positive instead of negative result, since the earth moves along positive values of the z axis.
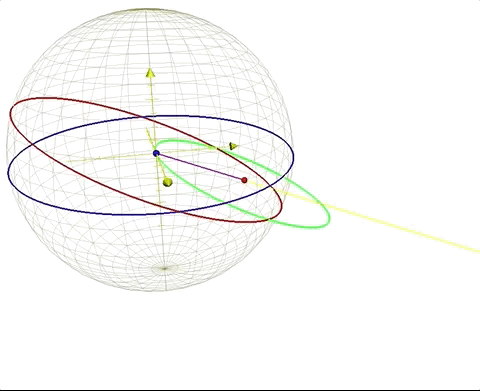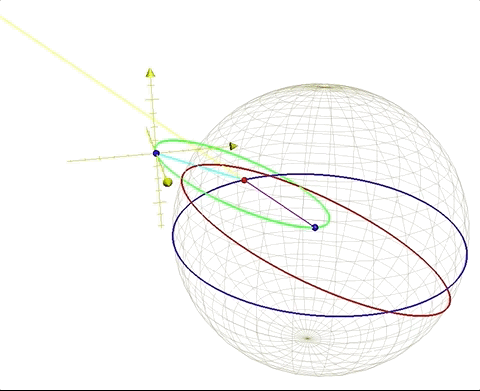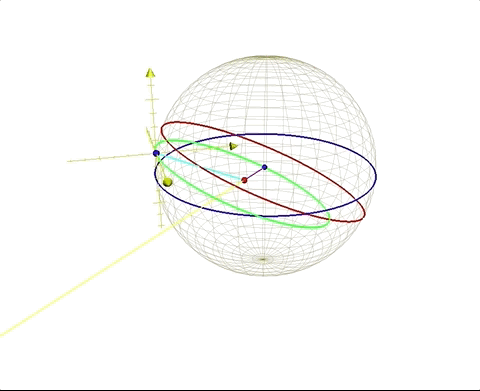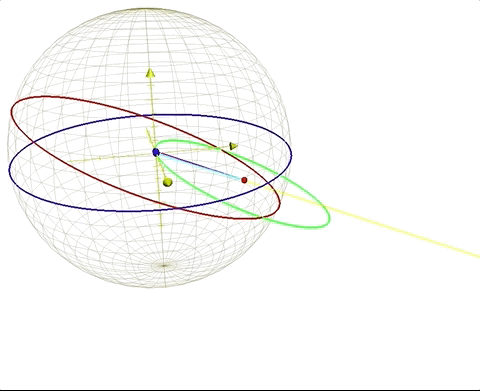
For our scenario, at the moment of departure for our journey, the moon is full and extending along the positive y axis, and dipping into negative z axis due to the tilt of the ecliptic. The yellow line in figures 5 and 6 below describes the angle and direction of the moon away from earth. β = angle ∠AQA' and is the amount the earth has orbited around the barycenter Q of the earth/moon system, with A as the starting location of the earth's center at time H = 0 (our time of gravity-free departure from the surface), and A' being the location of the earth's center after H hours of time. Clearly the movement of the earth along its barycentric orbit will change the location and distance of our closest point on earth as we journey on our gravity-free trajectory, and we will prepare the equations to find the correct values to describe our relationship to the earth's changing position in space as we move on our independent trajectory.
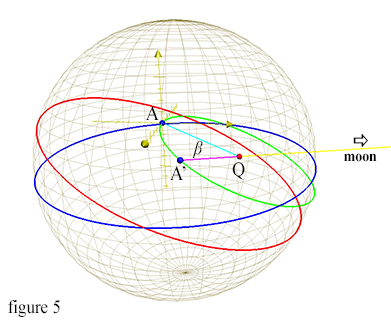
As the moon orbits the earth, the angle β increases along a 27.3 day sidereal cycle. In figure 5 above, angle β shows approximately 2 1/2 days of barycentric orbit, for diagram clarity. In this article we will be using a maximum time of six hours for our calculations. So for a six-hour period (H), the moon would have completed 0.0092 revolutions around the earth. Multiplying this by 2π gives us an angle β of 0.05754 radians, which we can see by
Where M is the length of the sidereal lunar orbit, or 27.3 days. In essence, these equations are fulfilling the same function as the equations that define the earth’s position along its solar orbit. Instead of the center of gravity being located at the sun with the earth wheeling around it, with the earth/moon system the center of gravity is within the earth itself, 4671 km from the center, represented by constant Be. We see this in figure 6 below, illustrated as the red point that always stays the same as the earth moves around this center, called the barycenter.
Δx would be sinβ, the value of a line connecting points A and A’. The value of is Δx not dependent of the inclination along the z axis of the ecliptic angle α (red great circle), described by the earth’s barycentric orbit around point Q. This is because the line of the ecliptic has its zero-intercept on the x axis, so the sine of any value of β would give us the proper Δx value. So
To find the Δy value of earth’s movement around the barycenter, we employ the cosine of angle β instead of ζ, which we used for earth's solar orbit calculations. 1 - cosβ will then give us change in y value, but since line AQ < 1 along the y axis due to the ecliptic angle α, we must multiply (1 - cosβ) * cosα to get the adjusted and correct value for Δy. And this we must multiply by Be/Re to turn the units compatible with our coordinate system with Re = 1.
The same process happens for Δz, but beginning with sinα to reflect the vertical aspect of the ecliptic angle α.
As the earth moves around the barycenter from A to A', each point on the earth's surface makes the same circular movement as the arc described by 
. The instantaneous velocity Vm of any point on, or within, the earth is found by
Where M = 27.3, or number of days in lunar sidereal month.
and its trajectory is always the at right angles to the line extending from line 
to the center of the moon. This velocity is imparted to us the moment we turn on our Grav-B-Gone, in addition to the velocity imparted to us by the rotation of the earth. For our purposes, since we leave at high noon, the value of Vm is only a vector along only the positive x axis, and an additive property to our tangential rotational velocity; hence our total velocity is Vm + cosL(Vr).
Now we are ready to put together all the motions into our calculations, and predict the closest point on earth to us at any time of our journey. What's more, we will look at three different departure points - one from the equator as we have discussed, but also departure points from latitude 45º (near upper Michigan), and latitude 90º, or the north pole. Our journey time will be six hours.
The blue lines are our gravity-free trajectories from the earth, and the green lines point to the earth's center, showing the closest point on earth to us, designate by a white point. The black great circle shows the rotation of the earth, and the yellow points show our departure locations on the earth's surface. Our positions during our gravity-free journeys are indicated by the red points, and the light blue points show our departure locations as fixed points in our coordinate system.
It is immediately apparent that the movement of the earth from its solar orbit, and from the earth/moon gravitational interaction, causes it to move along all three axes. We notice that the straight lines extending from our departure points have their origins located inside the earth as time progresses. We also see that our position during our trajectory from the north pole actually lies inside the earth for essentially the entire journey - by one minute our trajectory would place us 4.2 meters below the earth's surface, and with the icecap melting we would be in for a very cold bath. From the north pole trajectory we see the red point of our location actually lying under the surface of the earth, with the white point indicating the closest point to the earth's surface being above us instead of below.
Our goals will be the following: To find our distance to the closest point on earth below us at any moment in our journey (line 
in figure 8); and to find the distance on the earth's surface between our closest point on earth and the point of our departure as it moves with the earth's rotation (great circle arc between points D and B' in figure 10). Let's begin to work out the details. Figures 8, 9, and 10 below use the departure from latitude 45º as an example, to better show the angles involved.
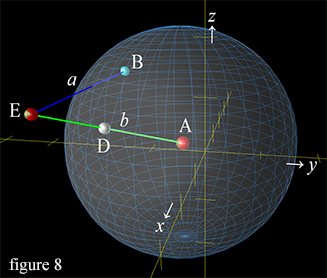
The first thing to do is to describe the line a that represents our gravity-free trajectory from the earth. Because we have chosen to leave at high noon, if you will, when the plane of our departure longitude line intersects the sun, this makes it much easier to calculate. Since our departure trajectories from latitudes 0º, 45º and 90º are all starting at x = 0, the tangent of the rotation of the earth at the moment of departure is exactly parallel to the x axis, for all three departure locations. The y and z values do not change as we move; from the equator y = cos0º or -1 throughout our journey, from latitude 45º y = cos45º or -0.7071, and from latitude 90º y = cos90º or 0. The z values remain at the sine of latitude of departure, or 0, 0.7071 and 1 respectively. So we simply move parallel to the x axis, at the velocity imparted to us by the earth's rotation, and by the barycentric rotation of the earth/moon system at the moment of departure, which we described above.
To find the closest point on earth to us at any point of our journey, we need draw line b from our point in space E (or in the case of the north pole trajectory, inside the earth) to the earth's center A. (Note that line b extends the entire length from point A to point E, intersecting point D). To draw this line we find the change in our x, y, and z coordinates at H hours after departure at our position at point E, from our present position as compared to the current location of the center of the earth.
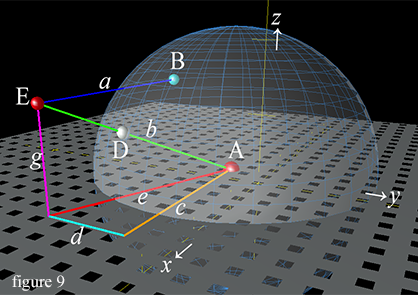
Before we can find the length of line b, we must draw lines c, d, e and g (figure 9), and use the pythagorean theorem to find the length of line b. Line c represents the change in x that line b describes from point A to point E, and line d represent line b's change in y value from point A to E, and line g represent the change in z value. However, we need to know the position of earth's center A, from which all lines orignate (line g also originates at the z value of point A). And point A is always moving.
We know the earth is moving the whole time from the earth/moon barycentric orbit, and from change in angle of the solar orbit. We have already calculated separately the movements caused by the earth's path along its solar orbit, and also the interactions with the moon, but now let's combine the two factors together to find each new x, y, and z position for earth after H hours. The first part of each equation represents the earth's motion from moon interaction, the second part repesents motion imparted by curve of solar orbit. So, the earth moves from its central starting position of 0, 0, 0 to a new position in space Ax, Ay and Az after H hours by:
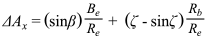
Where
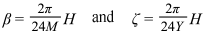
Since point A is not at position 0, 0, 0 when H > 0, we must subtract the x, y, and z values of point A from the respective x, y and z values of point E, to arrive at the length of lines c, d and g. To find the x coordinate for our position at E, or Ex:
Where
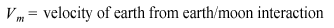
So to find the length for each line c, d and g we take:
and we know that the values for Ey and Ez do not change, since we are traversing only along the x axis during our journey; so Ey = -cosL and Ez = sinL. Then to find the length of line b, we first calculate the hypotenuse e from lines c and d, and then find the length of line b as the hypotenuse of lines e and g. We can do this in one step by:
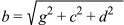
With that information in hand, now let's find the locations on the planet for the relevant points.
The latitude of point D, the closest point on earth to us, is the angle that line b rises from point A, which lies on the equatorial plane. So since g / b will give us the sine of ∠eb, then
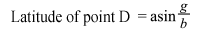
Point B' is the actual location on earth from which we departed, after the rotation of earth for a period of H hours (figure 10). The latitude B'lat of point B' remains 45º, represented by the purple latitude line, since our example uses the latitude 45º departure point.
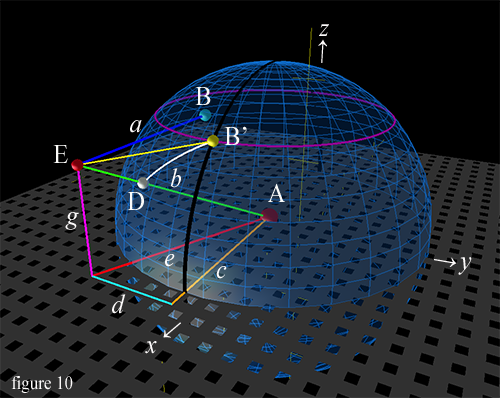
The black line represents the longitude line of our departure point as it rotates, so B'lon is the longitude for B, which of course is a fixed point on earth's surface and does not change. Here it is shown after six hours of our gravity-free journey, H = 6. Since we are using the sidereal day for our calculatons, the amount point B' has rotated is H / Sd or 0.2507 rotations of the earth at H = 6 hours. So the change in B'lon is 
.
What we want to do is find the difference in longitude between points B' and D, and this is just the angle between point D and point B' along the x-y plane. Now, since the earth has moved in space, the center of the earth A is no longer at position 0, 0, 0. We need the x distance between points A and D, which will be the sine of the angle expressed by the movement of D. This we produce by c / e, where c = (Ex - ΔAx), and e = the hypotenuse of lines c and d, or e = 
. So now we can take
to find the difference in angle between B' and D, along the x-y plane. We remember Ex is simply the distance we have moved parallel to the x axis, and Ex = H(Vm+ cosL(Vr)). The value of ∠DAB' is in radians, so to convert it to degrees showing the difference in angle between B'lon and Dlon we have:
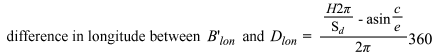
We now can generate both the latitude and longitude of both the closest point D to us on the earth's surface, and the currect location of our departure point B'. Now let's take a look at calculating the great circle distance between these two points on earth, just for fun. We'll say m = the great circle distance.
Where
Rea= 3671. or average radius of the earth
Let's break this down. With j and k we are basically finding the chord that connects points D and B' using the pythagorean theorem, by creating lines parallel to the x, y and z axes that define the positions of the two points. We see that j is an hypotenuse created using the x distance and the y distance lines (lines p and q in figure 11 below) as opposite and adjacent sides of a triangle. The first half of each squared entity in j defines the x and y values respectively of point B', and the second half of each squared entity in j represents the x and y values of point D. Then k finishes the process of creating the chord between the two points, again with the pythagorean theorem by finding the distance on the z axis between B' and D (line u), and defining the chord k as the hypotenuse of a second triangle with j and the distance on the z axis u as the opposite and adjacent sides.
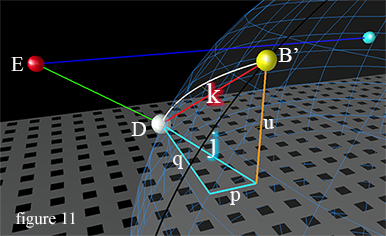
To help us visualize what we are doing, I've illustrated this in figure 11, where
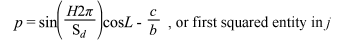
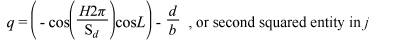
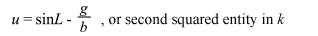
Allowing us to re-write the j and k as
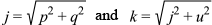
Which simplifies to
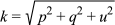
So now we have found the chord k that connects point B' and D, and m = (π - 2acos(k/2))Rea is the formula we need to find the arc m between these two points. This arc m is part of a great circle along the earth's surface, and is the shortest surface distance between our departure point B' and the closest point on earth to us, point D. So we have now completed our calculations and achieved our goals. Note that here we use the average circumference of the earth Rea to get the correct distance values.
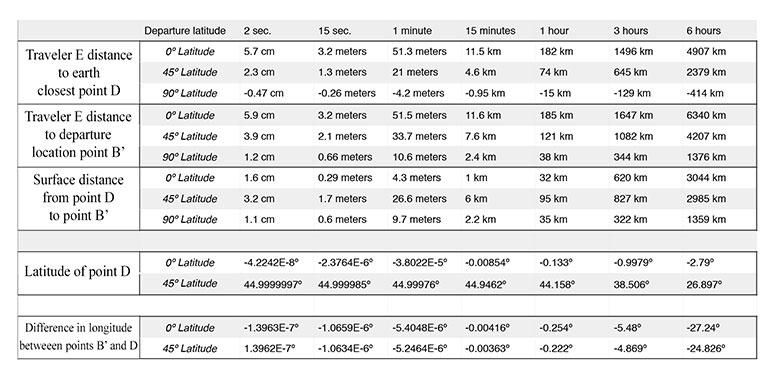
During a six-hour journey without gravity from our three departure points of 0º, 45º and 90º latitude, here is the data for all three scenarios. Note how the point D position of the traveler from the north pole is calculated to be inside the earth, as seen by the negative values for the closest point on earth, due to all the motions of the earth from sun and moon influences.
Using Google earth, I've entered some of the values from the chart above to give an idea of the trajectory for a latitude 45º departure. I've chosen a point in upper Michigan, on the shore in Grand Traverse Bay looking out into Lake Michigan.